LeetCode 二叉树
善用** ctrl+f**
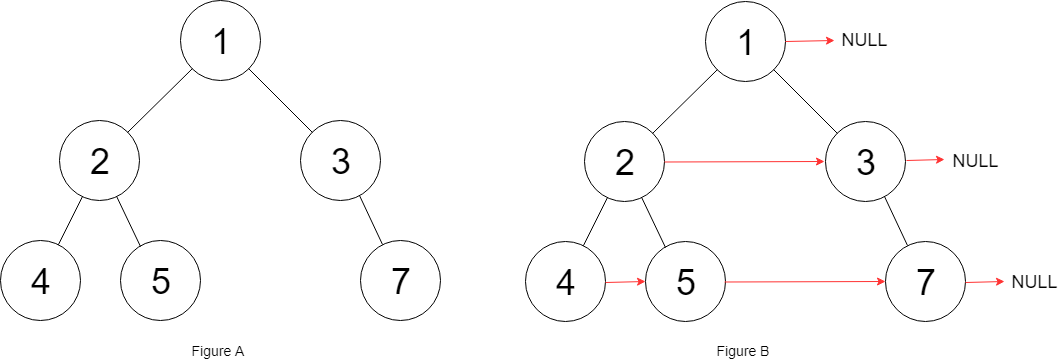
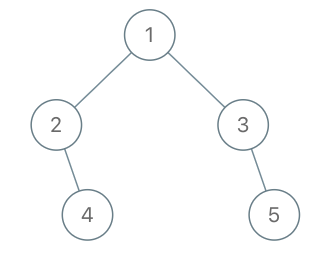
Given a binary tree, return the preorder traversal of its nodes’ values.
Example:
Input: [1 ,null ,2 ,3 ] 1 \ 2 / 3 Output: [1 ,2 ,3 ]
Follow up: Recursive solution is trivial, could you do it iteratively?
解法一
递归,没啥好说的
private List<Integer> res=new ArrayList <>();public List<Integer> preorderTraversal (TreeNode root) { if (root!=null ){ res.add(root.val); preorderTraversal(root.left); preorderTraversal(root.right); } return res; }
解法二
教科书上的写法,经典的前序遍历非递归实现方式
public List<Integer> preorderTraversal (TreeNode root) { List<Integer> res=new ArrayList <>(); if (root==null ) return res; Stack<TreeNode> stack=new Stack <>(); stack.push(root); while (!stack.isEmpty()){ TreeNode top=stack.pop(); res.add(top.val); if (top.right!=null ) { stack.push(top.right); } if (top.left!=null ) { stack.push(top.left); } } return res; }
解法三
非递归,模拟递归栈的方式,记录节点以及是否需要继续寻找子节点
public List<Integer> preorderTraversal (TreeNode root) { List<Integer> res=new ArrayList <>(); if (root==null ) return res; Stack<Command> stack=new Stack <>(); stack.push(new Command (true ,root)); while (!stack.isEmpty()){ Command command=stack.pop(); if (!command.isGo) { res.add(command.node.val); }else { TreeNode node=command.node; if (node.right!=null ) { stack.push(new Command (true ,node.right)); } if (node.left!=null ) { stack.push(new Command (true ,node.left)); } stack.push(new Command (false ,node)); } } return res; } static class Command { boolean isGo; TreeNode node; public Command (boolean isGo,TreeNode node) { this .isGo=isGo; this .node=node; } }
bobo 老师的一种思路,可以说是相当妙了👏,一下就解决了三种遍历的非递归实现,另外两种只需要调整一下进栈的顺序就可以了!
解法四
找到一个板子,可以很好的解决三种遍历
public List<Integer> preorderTraversal4 (TreeNode root) { List<Integer> res=new ArrayList <>(); if (root==null ) return res; Stack<TreeNode> stack=new Stack <>(); TreeNode cur=root; while (cur!=null ||!stack.isEmpty()){ while (cur!=null ) { res.add(cur.val); stack.push(cur); cur=cur.left; } cur=stack.pop(); cur=cur.right; } return res; }
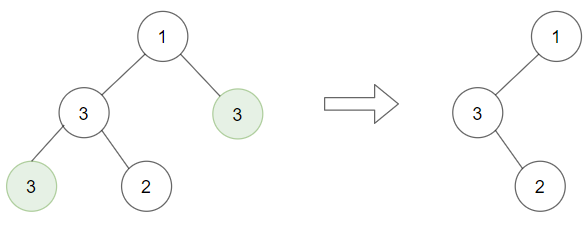
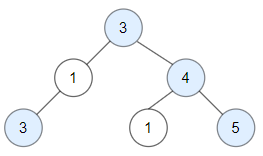
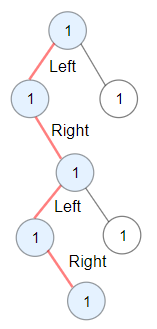
关于 while(cur!=null||!stack.isEmpty()),其实栈中存的只是某一个根节点的所有左子树,并不是所有的节点,所以栈为空不代表已经遍历完所有节点了,只能代表当前节点的左子树都遍历完了,还有右子树还没遍历,只有当右子树也为空也就是cur==null 的时候才是遍历完了,具体看一下下面这颗树就明白了
给定一个 N 叉树,返回其节点值的前序遍历 。
例如,给定一个 3 叉树 :
返回其前序遍历:[1,3,5,6,2,4]。
说明: 递归法很简单,你可以使用迭代法完成此题吗?
解法一
递归没啥好说的
List<Integer> res=new LinkedList <>(); public List<Integer> preorder (Node root) { dfs(root); return res; } public void dfs (Node root) { if (root==null ) { return ; } List<Node> children=root.children; res.add(root.val); for (Node node:children) { preorder(node); } }
解法二
迭代的方式
public List<Integer> preorder (Node root) { List<Integer> res=new LinkedList <>(); if (root==null ) { return res; } Stack<Node> stack=new Stack <>(); stack.add(root); while (!stack.isEmpty()){ Node node=stack.pop(); res.add(node.val); List<Node> children=node.children; for (int i=children.size()-1 ;i>=0 ;i--) { stack.add(children.get(i)); } } return res; }
到这里我是真的对遍历的那个板子无感了,这里我开始想用板子写,结果发现并不好写,无从下手(可能是我太菜),所以采用了经典的前序遍历方式,果然经典就是经典,通用性很强,而且相当好理解,所以以后遇到遍历的题目,尽量还是自己写,别套板子(对后序的板子也一直不是特别理解,所以也一直没记住,套板子还是要建立在理解的基础上啊,不然永远不会做!)
Given a binary tree, return the inorder traversal of its nodes’ values.
Example:
Input: [1 ,null ,2 ,3 ] 1 \ 2 / 3 Output: [1 ,3 ,2 ]
Follow up: Recursive solution is trivial, could you do it iteratively?
解法一
递归的方式和模拟栈的方式就不记录了,重点看一下这个板子
public List<Integer> inorderTraversal3 (TreeNode root) { List<Integer> res=new ArrayList <>(); if (root==null ) return res; Stack<TreeNode> stack=new Stack <>(); TreeNode cur=root; while (cur!=null ||!stack.isEmpty()){ while (cur!=null ) { stack.push(cur); cur=cur.left; } cur=stack.pop(); res.add(cur.val); cur=cur.right; } return res; }
Given a binary tree, return the postorder traversal of its nodes’ values.
Example:
Input: [1 ,null ,2 ,3 ] 1 \ 2 / 3 Output: [3 ,2 ,1 ]
Follow up: Recursive solution is trivial, could you do it iteratively?
解法一
这题是个 hard 题,没那么容易(不过根据 bobo 老师的方式来做确实简单😂)
public List<Integer> postorderTraversal3 (TreeNode root) { List<Integer> res=new ArrayList <>(); if (root==null ) return res; Stack<TreeNode> stack=new Stack <>(); TreeNode cur=root,lastNode=null ; while (cur!=null ||!stack.isEmpty()){ while (cur!=null ) { stack.push(cur); cur=cur.left; } cur=stack.peek(); if (cur.right==null ||cur.right==lastNode) { res.add(cur.val); lastNode=cur; stack.pop(); cur=null ; }else { cur=cur.right; } } return res; }
这种题一定要记住 “招式”,乱写只会越写越乱
解法二
这种解法似乎更加容易理解!!!
public List<Integer> postorderTraversals (TreeNode root) { List<Integer> res=new ArrayList <>(); if (root==null ) return res; Stack<TreeNode> stack=new Stack <>(); stack.push(root); TreeNode lastNode=null ; while (!stack.isEmpty()){ TreeNode cur=stack.peek(); if ((cur.left==null && cur.right ==null ) || (lastNode!=null &&( cur.left==lastNode || cur.right==lastNode))) { stack.pop(); res.add(cur.val); lastNode=cur; }else { if (cur.right!=null ) { stack.push(cur.right); } if (cur.left!=null ) { stack.push(cur.left); } } } return res; }
给定一个 N 叉树,返回其节点值的后序遍历 。
例如,给定一个 3 叉树 :
返回其后序遍历:[5,6,3,2,4,1].
说明: 递归法很简单,你可以使用迭代法完成此题吗?
解法一
递归的解法,没啥好说的
List<Integer> res=new LinkedList <>(); public List<Integer> postorder (Node root) { if (root==null ) { return res; } dfs(root); return res; } public void dfs (Node root) { List<Node> children=root.children; for (Node node:children) { dfs(node); } res.add(root.val); }
解法二
锁了!这才是树遍历的板子
public List<Integer> postorder (Node root) { List<Integer> res=new LinkedList <>(); if (root==null ) { return res; } Stack<Node> stack=new Stack <>(); stack.push(root); Node lastNode=null ; while (!stack.isEmpty()){ Node node=stack.peek(); List<Node> children=node.children; if (children.isEmpty() || (lastNode!=null && lastNode == children.get(children.size()-1 ))) { res.add(node.val); stack.pop(); lastNode=node; }else { for (int i=children.size()-1 ;i>=0 ;i--) { stack.push(children.get(i)); } } } return res; }
这题开始因为一个空的 case 把我搞晕了,搞了半天才发现
Given a binary tree, return the level order traversal of its nodes’ values. (ie, from left to right, level by level).
For example:[3,9,20,null,null,15,7],
return its level order traversal as:
解法一
BFS,利用队列
public List<List<Integer>> levelOrder (TreeNode root) { List<List<Integer>> res=new ArrayList <>(); if (root==null )return res; Queue<TreeNode> queue=new LinkedList <>(); queue.add(root); while (!queue.isEmpty()){ int count=queue.size(); List<Integer> list=new ArrayList <>(); while (count>0 ){ TreeNode node=queue.poll(); list.add(node.val); if (node.left!=null ) { queue.add(node.left); } if (node.right!=null ) { queue.add(node.right); } count--; } res.add(list); } return res; }
解法二
递归 DFS,这种其实还是挺有意思的,可以看下
public List<List<Integer>> levelOrder (TreeNode root) { List<List<Integer>> res = new ArrayList <>(); helper(res, root, 0 ); return res; } private void helper (List<List<Integer>> res, TreeNode root, int depth) { if (root == null ) return ; if (res.size() == depth) res.add(new LinkedList <>()); res.get(depth).add(root.val); helper(res, root.left, depth + 1 ); helper(res, root.right, depth + 1 ); }
给定一个 N 叉树,返回其节点值的层序遍历 。 (即从左到右,逐层遍历)。
例如,给定一个 3 叉树 :
返回其层序遍历:
说明:
树的深度不会超过 1000。
树的节点总数不会超过 5000。
解法一
public List<List<Integer>> levelOrder (Node root) { List<List<Integer>> res=new LinkedList <>(); if (root==null ) { return res; } Queue<Node> queue=new LinkedList <>(); queue.add(root); while (!queue.isEmpty()){ int count=queue.size(); List<Integer> temp=new LinkedList <>(); while (count>0 ){ Node node=queue.poll(); temp.add(node.val); for (Node child:node.children) { queue.add(child); } count--; } if (!temp.isEmpty()) { res.add(temp); } } return res; }
Given a binary tree, return the bottom-up level order traversal of its nodes’ values. (ie, from left to right, level by level from leaf to root).
For example:[3,9,20,null,null,15,7],
return its bottom-up level order traversal as:
解法一
public List<List<Integer>> levelOrderBottom (TreeNode root) { List<List<Integer>> res=new ArrayList <>(); if (root==null )return res; Queue<TreeNode> queue=new LinkedList <>(); queue.add(root); while (!queue.isEmpty()){ List<Integer> list=new ArrayList <>(); int count=queue.size(); while (count>0 ){ TreeNode top=queue.poll(); if (top.left!=null ) { queue.add(top.left); } if (top.right!=null ) { queue.add(top.right); } list.add(top.val); count--; } res.add(0 ,list); } return res; }
主要是复习下层次遍历,相比上面就多了 res.add(0,list) 从头部添加
Given a binary tree, return the zigzag level order traversal of its nodes’ values. (ie, from left to right, then right to left for the next level and alternate between).
For example:[3,9,20,null,null,15,7],
return its zigzag level order traversal as:
解法一
public List<List<Integer>> zigzagLevelOrder (TreeNode root) { List<List<Integer>> res=new ArrayList <>(); if (root==null )return res; Queue<TreeNode> queue=new LinkedList <>(); queue.add(root); boolean reverse=false ; while (!queue.isEmpty()){ LinkedList<Integer> list=new LinkedList <>(); int count=queue.size(); while (count>0 ){ TreeNode node=queue.poll(); if (reverse) { list.addFirst(node.val); }else { list.add(node.val); } if (node.left!=null ) { queue.add(node.left); } if (node.right!=null ) { queue.add(node.right); } count--; } reverse=!reverse; res.add(list); } return res; }
和上面一题一样,老想着怎么去按照题目的要求去遍历节点,哎,太蠢了,灵活一点啊
给定一棵二叉树,想象自己站在它的右侧,按照从顶部到底部的顺序,返回从右侧所能看到的节点值。
示例:
输入:[1 ,2 ,3 ,null ,5 ,null ,4 ] 输出:[1 , 3 , 4 ] 解释: 1 <--- / \ 2 3 <--- \ \ 5 4 <---
解法一
还是和上面一样,一上午做了三道一样的题,这题吸取了上面的教训没有去想怎么遍历了
public List<Integer> rightSideView (TreeNode root) { List<Integer> res=new ArrayList <>(); if (root==null ) return res; LinkedList<TreeNode> queue=new LinkedList <>(); queue.add(root); while (!queue.isEmpty()){ int count=queue.size(); while (count>0 ){ TreeNode node=queue.poll(); if (node.left!=null ) { queue.add(node.left); } if (node.right!=null ) { queue.add(node.right); } if (count==1 ) { res.add(node.val); } count--; } } return res; }
只记录每一层最后一个节点,最后得到的就是右视图
解法二
dfs,其实就是一直向右走,走不动就向左走,这样遍历的轨迹就是沿着二叉树的右边缘向下的,我们只需要记录层数,然后当层数和 res 数量相等的时候记录结果就行了(看见头条面试要求写 logN 空间的,应该就是这种解法了,但是下面的解法空间复杂度应该还是 O(N) 的,最坏情况下形成一链表就成 N 了,不过相比上面层次遍历永远是 N 的做法还是要好一点)
func rightSideView (root *TreeNode) int { var dfs func (root *TreeNode, depth int ) var res = make ([]int , 0 ) dfs = func (root *TreeNode, depth int ) if root == nil { return } if depth > len (res) { res = append (res, root.Val) } dfs(root.Right, depth+1 ) dfs(root.Left, depth+1 ) } dfs(root, 1 ) return res }
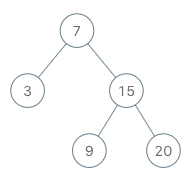
给定一个非空二叉树,返回一个由每层节点平均值组成的数组。
示例 1:
输入: 3 / \ 9 20 / \ 15 7 输出:[3 , 14.5 , 11 ] 解释: 第 0 层的平均值是 3 , 第 1 层是 14.5 , 第 2 层是 11. 因此返回 [3 , 14.5 , 11 ].
注意:
节点值的范围在 32 位有符号整数范围内。
解法一
一百遍啊一百遍,这应该属于树类型题的 HelloWorld 吧 ~
public List<Double> averageOfLevels (TreeNode root) { if (root==null ) { return new LinkedList <>(); } Queue<TreeNode> queue=new LinkedList <>(); List<Double> res=new ArrayList <>(); queue.add(root); while (!queue.isEmpty()) { int size=queue.size(); int temp=size; double average=0 ; while (size-->0 ){ TreeNode cur=queue.poll(); average+=cur.val; if (cur.left!=null ) { queue.add(cur.left); } if (cur.right!=null ) { queue.add(cur.right); } } average/=temp; res.add(average); } return res; }
给定一个二叉树,找出其最大深度。
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
说明: 叶子节点是指没有子节点的节点。
示例:
返回它的最大深度 3 。
解法一
递归解法,很简洁
public int maxDepth (TreeNode root) { if (root==null ){ return 0 ; } int maxLeft=maxDepth(root.left); int maxRight=maxDepth(root.right); return (maxLeft>maxRight?maxLeft:maxRight)+1 ; }
解法二
BFS,广度优先搜索
public int maxDepth (TreeNode root) { if (root==null ) return 0 ; Queue<TreeNode> queue=new LinkedList <>(); queue.add(root); int max=0 ; while (!queue.isEmpty()){ int count=queue.size(); while (count>0 ){ TreeNode node=queue.poll(); if (node.left!=null ) { queue.add(node.left); } if (node.right!=null ) { queue.add(node.right); } count--; } max++; } return max; }
给定一个 N 叉树,找到其最大深度。
最大深度是指从根节点到最远叶子节点的最长路径上的节点总数。
例如,给定一个 3 叉树 :
我们应返回其最大深度,3。
说明:
树的深度不会超过 1000。
树的节点总不会超过 5000。
解法一
没啥好说的
public int maxDepth (Node root) { if (root==null ) { return 0 ; } int max=0 ; List<Node> children=root.children; for (Node node:children) { max=Math.max(max,maxDepth(node)); } return max+1 ; }
给定一个二叉树,找出其最小深度。
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
说明: 叶子节点是指没有子节点的节点。
示例:
给定二叉树 [3,9,20,null,null,15,7]
返回它的最小深度 2.
解法一
最大都求了,最小也来一发,经典 BFS 做法,求最短路径
public int minDepth (TreeNode root) { if (root==null ) return 0 ; Queue<TreeNode> queue=new LinkedList <>(); queue.add(root); int min=0 ; while (!queue.isEmpty()){ int count=queue.size(); min++; while (count>0 ){ TreeNode node=queue.poll(); if (node.left==null && node.right==null ) { return min; } if (node.left!=null ) { queue.add(node.left); } if (node.right!=null ) { queue.add(node.right); } count--; } } return min; }
解法二
递归
public int minDepth (TreeNode root) { if (root==null ) return 0 ; if (root.left==null ) { return minDepth(root.right)+1 ; } if (root.right==null ) { return minDepth(root.left)+1 ; } return Math.min(minDepth(root.left),minDepth(root.right))+1 ; }
很上面最大的相反,但是有个细节需要注意,如果一个根节点左右子树,有一颗为空 ,如果不处理,按照之前的逻辑,这颗空子树下一次就会返回 0,肯定会比另一颗小最后返回的就是到这颗子树的路径,但是仔细想想这样是正确的么?明显不是,最短路径的尽头一定是叶子节点也就是左右子树都为空的时候,所以这里需要特别注意
翻转一棵二叉树。
示例:
输入:
输出:
备注:
谷歌:我们 90%的工程师使用您编写的软件 (Homebrew),但是您却无法在面试时在白板上写出翻转二叉树这道题,这太糟糕了。
解法一
public TreeNode invertTree (TreeNode root) { if (root==null ) { return null ; } invertTree(root.left); invertTree(root.right); TreeNode temp=root.left; root.left=root.right; root.right=temp; return root; }
注意递归调用和交换节点的顺序,不能搞反了
public TreeNode invertTree (TreeNode root) { if (root==null ) { return null ; } TreeNode right=root.right; root.right=invertTree(root.left); root.left=invertTree(right); return root; }
比较简洁也比较符合递归的做法
给定两个二叉树,编写一个函数来检验它们是否相同。
如果两个树在结构上相同,并且节点具有相同的值,则认为它们是相同的。
示例 1:
输入:1 1 / \ / \ 2 3 2 3 [1 ,2 ,3 ], [1 ,2 ,3 ] 输出:true
示例 2:
输入:1 1 / \ 2 2 [1 ,2 ], [1 ,null ,2 ] 输出:false
示例 3:
输入:1 1 / \ / \ 2 1 1 2 [1 ,2 ,1 ], [1 ,1 ,2 ] 输出:false
解法一
public boolean isSameTree (TreeNode p, TreeNode q) { if (p==null && q==null ) { return true ; } if (p!=null && q!=null && p.val==q.val) { return isSameTree(p.right,q.right)&&isSameTree(p.left,q.left); } return false ; }
Difficulty: 中等
我们可以为二叉树 T 定义一个翻转操作,如下所示:选择任意节点,然后交换它的左子树和右子树。
只要经过一定次数的翻转操作后,能使 X 等于 Y,我们就称二叉树 X _翻转等价_于二叉树 Y。
编写一个判断两个二叉树是否是_翻转等价_的函数。这些树由根节点 root1 和 root2 给出。
示例:
输入:root1 = [1 ,2 ,3 ,4 ,5 ,6 ,null,null,null,7 ,8 ], root2 = [1 ,3 ,2 ,null,6 ,4 ,5 ,null,null,null,null,8 ,7 ] 输出:true 解释:我们翻转值为 1 ,3 以及 5 的三个节点。
提示:
每棵树最多有 100 个节点。
每棵树中的每个值都是唯一的、在 [0, 99] 范围内的整数。
解法一
交错的比较就行了
func flipEquiv (root1 *TreeNode, root2 *TreeNode) bool { if root1 == nil && root2 == nil { return true } if root1 == nil || root2 == nil { return false } if root1.Val != root2.Val { return false } return (flipEquiv(root1.Left, root2.Left) && flipEquiv(root1.Right, root2.Right)) || (flipEquiv(root1.Left, root2.Right) && flipEquiv(root1.Right, root2.Left)) }
给定两个非空二叉树 s 和 t,检验 s 中是否包含和 t 具有相同结构和节点值的子树。s 的一个子树包括 s 的一个节点和这个节点的所有子孙。s 也可以看做它自身的一棵子树。
示例 1:
给定的树 t:
返回 true ,因为 t 与 s 的一个子树拥有相同的结构和节点值。
示例 2:
给定的树 t:
返回 false
解法一
先上一个错误解法
public boolean isSubtree (TreeNode s, TreeNode t) { if (t==null && s==null ) { return true ; } if (s==null ) { return false ; } if (s!=null && t!=null && s.val == t.val) { return isSubtree(s.left,t.left) && isSubtree(s.right,t.right); } return isSubtree(s.left,t) | isSubtree(s.right,t); }
过了 146/176 的 case,但是这个明显是错的,不过核心的递归还是大概雏形写出来了
解法二
思考了一会,光速瞄了一眼评论区,隐约看到了有人说双递归,然后想到了下面的解
public boolean isSubtree (TreeNode s, TreeNode t) { if (s==null ) { return false ; } return isSame(s,t)| isSubtree(s.left,t) | isSubtree(s.right,t); } public boolean isSame (TreeNode s, TreeNode t) { if (s==null && t==null ) { return true ; } if (s==null || t==null ) { return false ; } return s.val==t.val && isSame(s.left,t.left) && isSame(s.right,t.right); }
开始的代码没这么简洁,比较罗嗦,要判断一棵树是不是另一颗的子树很好判断,要么 s 和 t 直接相等,要么 t 是 s 左子树的子树,或者右子树的子树,所以我们还需要一个函数判断两个两棵树是否相等,只用一个函数确实不好实现
解法三
其实还有一种解法,也是最开始想到的,就是直接中序遍历和前序遍历,得到两个序列,然后用 kmp 匹配两棵树,kmp 很久没看了,不会写了,后面有时间再来写
输入两棵二叉树 A 和 B,判断 B 是不是 A 的子结构。(约定空树不是任意一个树的子结构)
B 是 A 的子结构, 即 A 中有出现和 B 相同的结构和节点值。
例如:
给定的树 B:
返回 true,因为 B 与 A 的一个子树拥有相同的结构和节点值。
示例 1:
输入:A = [1 ,2 ,3 ], B = [3 ,1 ] 输出:false
示例 2:
输入:A = [3 ,4 ,5 ,1 ,2 ], B = [4 ,1 ] 输出:true
限制:
0 <= 节点个数 <= 10000
解法一
一样的题为啥还加上?仔细看题,我开始也以为是一样的
public boolean isSubStructure (TreeNode A, TreeNode B) { if (A==null || B==null ){ return false ; } return isSame(A,B) | isSubStructure(A.left,B) | isSubStructure(A.right,B); } public boolean isSame (TreeNode A,TreeNode B) { if (B==null ) { return true ; } if (A==null ){ return false ; } return A.val==B.val && isSame(A.left,B.left) && isSame(A.right,B.right); }
这里说的是子结构不是子树,isSame 函数不需要保证完全相等,这里就需要注意了,当A!=null && B==null的时候就说明 B 已经匹配完了 A 还没有,这就说明 B 是 A 的子结构
UPDATE(2020.5.7)
换了一下写法,不用考虑顺序了
func isSubStructure (A *TreeNode, B *TreeNode) bool { if B==nil || A==nil { return false } return dfs(A,B) || isSubStructure(A.Left,B) || isSubStructure(A.Right,B) } func dfs (A *TreeNode, B *TreeNode) bool { if A==nil && B==nil { return true } if A==nil || B==nil { return B==nil } return A.Val==B.Val && dfs(A.Left,B.Left) && dfs(A.Right,B.Right) }
给出一个完全二叉树 ,求出该树的节点个数。
说明:
完全二叉树的定义如下:在完全二叉树中,除了最底层节点可能没填满外,其余每层节点数都达到最大值,并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层,则该层包含 1~ 2h 个节点。
示例:
输入: 1 / \ 2 3 / \ / 4 5 6 输出:6
解法一
BFS,权当复习了
public int countNodes (TreeNode root) { Queue<TreeNode> queue=new LinkedList <>(); if (root == null ) return 0 ; queue.add(root); int count=1 ; while (!queue.isEmpty()){ int nextLevel=queue.size(); while (nextLevel>0 ){ TreeNode node=queue.poll(); count++; if (node.left!=null ) { queue.add(node.left); } if (node.right!=null ) { queue.add(node.right); } nextLevel--; } } return count; }
解法二
递归解法
public int countNodes (TreeNode root) { if (root==null ) return 0 ; return countNodes(root.left)+countNodes(root.right)+1 ; }
更加精简点可以缩减成一行
解法三
这题是 mid 难度,而且题目给的条件还没用上:这是一颗完全二叉树 ,所以我们可以利用它的性质来做,众所周知,满二叉树的节点个数 可以直接根据公式 2^H-1 计算得来,所以我们只要判断当前的完全二叉树是不是满二叉树 ,如果是直接算出来,这样就可以省去中间很多节点的遍历
public int countNodes (TreeNode root) { if (root==null ) return 0 ; TreeNode left=root.left; TreeNode right=root.right; int hight=0 ; while (left!=null && right!=null ){ left=left.left; right=right.right; hight++; } return left==null ?(1 <<hight)-1 :countNodes(root.left)+countNodes(root.right)+1 ; }
不得不说这样的方式还是挺巧妙的,时间复杂度应该是O(2logN)?
给定一个二叉树和一个目标和,判断该树中是否存在根节点到叶子节点 的路径,这条路径上所有节点值相加等于目标和。
说明: 叶子节点是指没有子节点的节点。
示例: sum = 22
5 / \ 4 8 / / \ 11 13 4 / \ \ 7 2 1
返回 true, 因为存在目标和为 22 的根节点到叶子节点的路径 5->4->11->2
解法一
递归解法
public boolean hasPathSum (TreeNode root, int sum) { if (root==null ) { return false ; } if (root.left==null && root.right==null &&root.val==sum) { return true ; } return hasPathSum(root.left,sum-root.val) || hasPathSum(root.right,sum-root.val); }
值得注意的地方就是这个叶子节点的判断,一开始没注意到,直接写的 root.val==sum ,其实如果不是叶子节点的话,其实是不成立的,比如
其实这就是false ,因为他没有右子树,而题目要求的是从根节点到叶子节点
计算给定二叉树的所有左叶子之和。
示例:
在这个二叉树中,有两个左叶子,分别是 9 和 15,所以返回 24
解法一
说实话,这些题给的例子都挺误导人的,会让人不自觉地忽略叶子节点 这个条件😂
private int sum=0 ;public int sumOfLeftLeaves (TreeNode root) { sumOfLeft(root); return sum; }; public void sumOfLeft (TreeNode root) { if (root==null ) { return ; } if (root.left!=null && root.left.left==null &&root.left.right==null ) { sum+=root.left.val; } sumOfLeft(root.left); sumOfLeft(root.right); }
给定一个二叉树,返回所有从根节点到叶子节点的路径。
说明: 叶子节点是指没有子节点的节点。
示例:
输入: 1 / \ 2 3 \ 5 输出:["1->2->5" , "1->3" ] 解释:所有根节点到叶子节点的路径为:1 ->2 ->5 , 1 ->3
解法一
递归 DFS 的解法
public List<String> binaryTreePaths (TreeNode root) { List<String> res=new ArrayList <>(); if (root==null ) return res; if (root!=null &&root.left==null &&root.right==null ) { res.add(String.valueOf(root.val)); return res; } List<String> lefts=binaryTreePaths(root.left); List<String> rights=binaryTreePaths(root.right); for (int i=0 ;i<lefts.size();i++) { res.add(root.val+"->" +lefts.get(i)); } for (int i=0 ;i<rights.size();i++) { res.add(root.val+"->" +rights.get(i)); } return res; }
比上面的递归稍微复杂点,核心思想还是要抓住递归的本质,不要去纠结递归每一步都是怎么得到的,从宏观上去写代码,还是要多练啊
解法二
BFS 广搜
public List<String> binaryTreePaths (TreeNode root) { List<String> res=new ArrayList <>(); if (root==null ) return res; Stack<TreeNode> node_stack=new Stack <>(); Stack<String> path_stack=new Stack <>(); node_stack.add(root); path_stack.add(String.valueOf(root.val)); String path="" ; while (!node_stack.isEmpty()){ TreeNode node=node_stack.pop(); path=path_stack.pop(); if (node.left==null &&node.right==null ) { res.add(path); } if (node.left!=null ) { node_stack.add(node.left); path_stack.add(path+"->" +node.left.val); } if (node.right!=null ) { node_stack.add(node.right); path_stack.add(path+"->" +node.right.val); } } return res; }
这里和传统的 BFS 不太一样,是用的栈来遍历的
解法三
这种解法应该会比上面的解法复杂度低一点
func binaryTreePaths (root *TreeNode) string { var res []string dfs(root,"" ,&res) return res } func dfs (root *TreeNode,path string ,res *[]string ) if root==nil {return } path+=strconv.Itoa(root.Val) if root.Left==nil && root.Right==nil { *res=append (*res,path) return } dfs(root.Left,path+"->" ,res) dfs(root.Right,path+"->" ,res) }
给定一个二叉树和一个目标和,找到所有从根节点到叶子节点路径总和等于给定目标和的路径。
说明: 叶子节点是指没有子节点的节点
示例: sum = 22,
5 / \ 4 8 / / \ 11 13 4 / \ / \ 7 2 5 1
返回:
解法一
和上一题的做法基本一致,本来应该是一遍 bugfree 的,编译错误整了半天
public List<List<Integer>> pathSum (TreeNode root, int sum) { List<List<Integer>> res=new LinkedList <>(); if (root==null ) { return res; } if (root!=null && root.left==null && root.right==null && root.val==sum) { LinkedList<Integer> lis= new LinkedList <>(); lis.add(root.val); res.add(lis); return res; } List<List<Integer>> lefts=pathSum(root.left,sum-root.val); List<List<Integer>> rights=pathSum(root.right,sum-root.val); for (int i=0 ;i<lefts.size();i++) { ((LinkedList<Integer>)lefts.get(i)).addFirst(root.val); res.add(lefts.get(i)); } for (int i=0 ;i<rights.size();i++) { ((LinkedList<Integer>)rights.get(i)).addFirst(root.val); res.add(rights.get(i)); } return res; }
解法二
废了老大劲终于把 BFS 写出来了。可以看出还是借鉴的上面的思路
public List<List<Integer>> pathSum2 (TreeNode root,int sum) { List<List<Integer>> res=new LinkedList <>(); if (root==null ) return res; Stack<TreeNode> node_stack=new Stack <>(); Stack<List<Integer>> path_stack=new Stack <>(); Stack<Integer> sum_stack=new Stack <>(); node_stack.add(root); path_stack.add(new LinkedList (){{ add(root.val); }}); sum_stack.add(root.val); while (!node_stack.isEmpty()){ TreeNode node=node_stack.pop(); List<Integer> pathList=path_stack.pop(); int tempS=sum_stack.pop(); if (node.left==null && node.right==null &&tempS==sum) { res.add(pathList); continue ; } if (node.left!=null ) { node_stack.add(node.left); LinkedList<Integer> tlis= new LinkedList (pathList); tlis.add(node.left.val); path_stack.add(tlis); sum_stack.add(tempS+node.left.val); } if (node.right!=null ) { node_stack.add(node.right); LinkedList<Integer> tlis= new LinkedList (pathList); tlis.add(node.right.val); path_stack.add(tlis); sum_stack.add(tempS+node.right.val); } } return res; }
用到三个栈,同步保存节点的信息,还是挺简单的
解法三
补一种 dfs+回溯的思路,上面的所有路径也可以这样做,感觉会比上面的要好一点
public List<List<Integer>> pathSum (TreeNode root, int sum) { dfs(root,sum,new ArrayList <>()); return res; } private List<List<Integer>> res=new ArrayList <>();public void dfs (TreeNode root,int sum,List<Integer> lis) { if (root==null ) return ; lis.add(root.val); if (root.left==null && root.right==null && sum==root.val){ res.add(new ArrayList (lis)); }else { dfs(root.left,sum-root.val,lis); dfs(root.right,sum-root.val,lis); } lis.remove(lis.size()-1 ); }
满二叉树 是一类二叉树,其中每个结点恰好有 0 或 2 个子结点。
返回包含 N 个结点的所有可能满二叉树的列表。 答案的每个元素都是一个可能树的根结点。
答案中每个树的每个结点都必须 有 node.val=0。
你可以按任何顺序返回树的最终列表。
示例:
输入:7 输出:[[0 ,0 ,0 ,null ,null ,0 ,0 ,null ,null ,0 ,0 ],[0 ,0 ,0 ,null ,null ,0 ,0 ,0 ,0 ],[0 ,0 ,0 ,0 ,0 ,0 ,0 ],[0 ,0 ,0 ,0 ,0 ,null ,null ,null ,null ,0 ,0 ],[0 ,0 ,0 ,0 ,0 ,null ,null ,0 ,0 ]] 解释:
提示:
解法一
这题和上面两题很类似,可惜我并没有直接做出来,菜啊,看了一眼评论区看见了几个 for 循环立马就懂了,然后过了好几天实现了下,一开始 root 的位置放错了,改了一会儿
public List<TreeNode> allPossibleFBT (int N) { List<TreeNode> res=new ArrayList <>(); if (N%2 ==0 ) return res; if (N==1 ){ res.add(new TreeNode (0 )); return res; } N--; for (int i=1 ;i<N;i+=2 ){ List<TreeNode> lefts=allPossibleFBT(i); List<TreeNode> rights=allPossibleFBT(N-i); for (TreeNode le:lefts){ for (TreeNode ri:rights){ TreeNode root=new TreeNode (0 ); root.left=le; root.right=ri; res.add(root); } } } return res; }
给定一个二叉树,它的每个结点都存放一个 0-9 的数字,每条从根到叶子节点的路径都代表一个数字。
例如,从根到叶子节点路径 1->2->3 代表数字 123
计算从根到叶子节点生成的所有数字之和。
说明: 叶子节点是指没有子节点的节点。
示例 1:
输入:[1 ,2 ,3 ] 1 / \ 2 3 输出:25 解释: 从根到叶子节点路径 1 ->2 代表数字 12. 从根到叶子节点路径 1 ->3 代表数字 13. 因此,数字总和 = 12 + 13 = 25.
示例 2:
输入:[4 ,9 ,0 ,5 ,1 ] 4 / \ 9 0 / \ 5 1 输出:1026 解释: 从根到叶子节点路径 4 ->9 ->5 代表数字 495. 从根到叶子节点路径 4 ->9 ->1 代表数字 491. 从根到叶子节点路径 4 ->0 代表数字 40. 因此,数字总和 = 495 + 491 + 40 = 1026.
解法一
BFS,延续上面的做法
public int sumNumbers (TreeNode root) { int res=0 ; if (root == null ) return res; Stack<TreeNode> node_stack=new Stack <>(); Stack<Integer> sum_stack=new Stack <>(); node_stack.add(root); sum_stack.add(root.val); while (!node_stack.isEmpty()){ TreeNode node=node_stack.pop(); int tempS=sum_stack.pop(); if (node.left==null && node.right==null ) { res+=tempS; continue ; } if (node.left!=null ) { node_stack.add(node.left); sum_stack.add(tempS*10 +node.left.val); } if (node.right!=null ) { node_stack.add(node.right); sum_stack.add(tempS*10 +node.right.val); } } return res; }
解法二
DFS 解法,一开始没想出来。
private int sum=0 ;public int sumNumbers2 (TreeNode root) { sumNumber(0 ,root); return sum; } public void sumNumber (int parent,TreeNode root) { if (root==null ) { return ; } int cur=parent*10 +root.val; if (root!=null && root.left==null && root.right==null ) { sum+=cur; } sumNumber(cur,root.left); sumNumber(cur,root.right); }
给出一棵二叉树,其上每个结点的值都是 0 或 1 。每一条从根到叶的路径都代表一个从最高有效位开始的二进制数。例如,如果路径为 0 -> 1 -> 1 -> 0 -> 1,那么它表示二进制数 01101,也就是 13 。
对树上的每一片叶子,我们都要找出从根到该叶子的路径所表示的数字。
以 10^9 + 7 为模 ,返回这些数字之和。
示例:
输入:[1 ,0 ,1 ,0 ,1 ,0 ,1 ] 输出:22 解释:(100 ) + (101 ) + (110 ) + (111 ) = 4 + 5 + 6 + 7 = 22
提示:
树中的结点数介于 1 和 1000 之间。
node.val 为 0 或 1 。
解法一
和上一题一摸一样,没啥好说的,只不过一个是 10 进制,一个是二进制
var mod=int (1e9 +7 )func sumRootToLeaf (root *TreeNode) int { sum:=0 ; dfs(root,0 ,&sum) return sum } func dfs (root *TreeNode,cur int ,sum *int ) if root==nil { return } cur=(cur<<1 +root.Val)%mod if root!=nil && root.Left==nil && root.Right==nil { *sum=(*sum+cur)%mod return } dfs(root.Left,cur,sum) dfs(root.Right,cur,sum) }
这题的数据太弱了,甚至都不用取模照样可以过。我一开始看到 1000 个节点,还考虑要不要处理大数的情况,看到返回值是 int 才作罢🤣
给定一个二叉树,它的每个结点都存放着一个整数值。
找出路径和等于给定数值的路径总数。
路径不需要从根节点开始,也不需要在叶子节点结束,但是路径方向必须是向下的(只能从父节点到子节点)。
二叉树不超过 1000 个节点,且节点数值范围是 [-1000000,1000000] 的整数。
示例:
root = [10 ,5 ,-3 ,3 ,2 ,null ,11 ,3 ,-2 ,null ,1 ], sum = 8 10 / \ 5 -3 / \ \ 3 2 11 / \ \ 3 -2 1
返回 3。和等于 8 的路径有:
5 -> 3
5 -> 2 -> 1
-3 -> 11
解法一
public int pathSum (TreeNode root, int sum) { if (root == null ) { return 0 ; } int res=findPath(root,sum); res+=pathSum(root.left,sum); res+=pathSum(root.right,sum); return res; } public int findPath (TreeNode node,int sum) { int res=0 ; if (node==null ) { return res; } if (node.val==sum) { res++; } res+=findPath(node.left,sum-node.val); res+=findPath(node.right,sum-node.val); return res; }
emmmm,这题分类是 easy 确实太迷了,嵌套的递归,看了解法确实看的懂,但是写是绝对写不出来的(眼睛:我懂了,脑子:你懂个锤子)除非能记住
回头来看发现其实挺简单的,确实是 easy 题~ 但是这个解很明显不是最优解,这个里面会有很多的重复的计算,最优解是利用 前缀和+回溯的解法,有点小顶~
解法二
补上前缀和的做法,之前好像是看了答案,然后感觉很难,就没写?今天又重新做了下,先写了暴力解,然后就直接写出了前缀和的做法,感觉前缀和的思路还是挺优秀的,一开始忘了回溯,思考了下意识到这里记录的应该是一条分支之上而下的前缀和,所以在统计完某个节点后应该回溯
func pathSum (root *TreeNode, sum int ) int { if root == nil { return 0 } var res = 0 var preSum = make (map [int ]int ) preSum[0 ] = 1 dfs(root, 0 , sum, preSum, &res) return res } func dfs (root *TreeNode, sum int , target int , preSum map [int ]int , res *int ) if root == nil { return } sum += root.Val *res += preSum[sum-target] preSum[sum]++ dfs(root.Left, sum, target, preSum, res) dfs(root.Right, sum, target, preSum, res) preSum[sum]-- }
给定一个二叉搜索树,找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先 )
例如,给定如下二叉搜索树:root = [6,2,8,0,4,7,9,null,null,3,5]
示例 1:
输入:root = [6 ,2 ,8 ,0 ,4 ,7 ,9 ,null ,null ,3 ,5 ], p = 2 , q = 8 输出:6 解释:节点 2 和节点 8 的最近公共祖先是 6
示例 2:
输入:root = [6 ,2 ,8 ,0 ,4 ,7 ,9 ,null ,null ,3 ,5 ], p = 2 , q = 4 输出:2 解释:节点 2 和节点 4 的最近公共祖先是 2 , 因为根据定义最近公共祖先节点可以为节点本身。
说明:
所有节点的值都是唯一的。
p、q 为不同节点且均存在于给定的二叉搜索树中。
解法一
看了一点点思路,然后 bugfree
public TreeNode lowestCommonAncestor (TreeNode root, TreeNode p, TreeNode q) { if (p.val<root.val && q.val<root.val) { return lowestCommonAncestor(root.left,p,q); }else if (p.val > root.val && q.val > root.val) { return lowestCommonAncestor(root.right,p,q); }else { return root; } }
其实核心就是利用好 BST 的性质,左子树一定小于根节点,右子树一定大于根节点,求公共祖先,如果一个节点在左子树,一个在右子树,那么最近的公共祖先一定是 root,除此之外,还有一种特殊情况就是当两个节点已经有祖先关系的时候,那么直接返回祖先节点就可以了
这里其实前面的if可以去掉,题目中说到了所有节点的值都是唯一的,所以节点值相等就说明是同一个节点,就已经包含在最后一个 else 的情况中了
给定一个二叉树,判断其是否是一个有效的二叉搜索树。
假设一个二叉搜索树具有如下特征:
节点的左子树只包含小于 当前节点的数。
节点的右子树只包含大于 当前节点的数。
所有左子树和右子树自身必须也是二叉搜索树。
示例 1:
示例 2:
输入: 5 / \ 1 4 / \ 3 6 输出:false 解释:输入为:[5 ,1 ,4 ,null ,null ,3 ,6 ]。 根节点的值为 5 ,但是其右子节点值为 4
解法一
递归解法,很巧妙
public boolean isValidBST (TreeNode root) { if (root==null ) { return true ; } return isValidBST(root,null ,null ); } public boolean isValidBST (TreeNode node,Integer low,Integer high) { if (node==null ) return true ; if (low!=null && low>=node.val || high!=null && high<=node.val) { return false ; } return isValidBST(node.left,low,node.val) && isValidBST(node.right,node.val,high); }
一定要注意 BST 的性质是根节点大于所有 右子树的节点,小于所有 左子树的节点,而不是简单的验证当前节点和左右节点的大小关系就可以了,所以我们在验证的时候传入对应的上界 和下界 ,节点必须要大于下界,小于上界,那么上界和下界从哪里来?当前节点就是左子树的上界,右子树的下界! 然后递归左右子树就 ok 了
这题其实还有一个坑,只不过我这个做法直接跳过了,题目的 case 中有的节点值是Integer.MIN_VALUE,和Integer.MAX_VALUE ,如果上界下界直接用 int 来传递的话,很有可能递归初始调用就是这样的
return isValidBST(root,Integer.MIN_VALUE,Integer.MAX_VALUE); 这就正中出题人下怀,所以我们这里用一个包装类型,这样我们只需要检测上界下界是不是 null 就可以了
解法二
这个就利用了 BST 和中序遍历的关系,我们知道中序遍历是 左->根->右 这个顺序放到 BST 中恰好就是一个升序的序列,所以我们就可以利用这个性质来判断二叉树是不是 BST
public boolean isValidBST (TreeNode root) { LinkedList<Integer> order=new LinkedList <>(); if (root==null ) { return true ; } Stack<TreeNode> stack=new Stack <>(); TreeNode cur=root; while (cur!=null || !stack.isEmpty()){ while (cur!=null ){ stack.add(cur); cur=cur.left; } cur=stack.pop(); if (!order.isEmpty() && order.getLast()>= cur.val) { return false ; } order.add(cur.val); cur=cur.right; } return true ; }
这里其实可以不用 list 保存结果,用一个 int 保存上一次的节点值就行了 md 重做的时候因为这个 WA 了好几次,如果用 int 的话需要加一个标志位用来初始化
Difficulty: 中等
给定一个二叉树,确定它是否是一个_完全二叉树_。
中对完全二叉树的定义如下:
若设二叉树的深度为 h,除第 h 层外,其它各层 (1~h-1) 的结点数都达到最大个数,第 h 层所有的结点都连续集中在最左边,这就是完全二叉树。(注:第 h 层可能包含 1~ 2h 个节点。)
示例 1:
输入:[1 ,2 ,3 ,4 ,5 ,6 ] 输出:true 解释:最后一层前的每一层都是满的(即,结点值为 {1 } 和 {2 ,3 } 的两层),且最后一层中的所有结点({4 ,5 ,6 })都尽可能地向左。
示例 2:
输入:[1 ,2 ,3 ,4 ,5 ,null,7 ] 输出:false 解释:值为 7 的结点没有尽可能靠向左侧。
提示:
树中将会有 1 到 100 个结点。
解法一
一开始思路出现了问题,想着去按照节点个数去校验,然后对最后一层做特判,然后发现这种思路是死胡同,实际上判断是否是完全二叉树很简单,只要节点中间 没有出现 null 就说明是完全二叉树
public boolean isCompleteTree (TreeNode root) { if (root == null ) { return true ; } Queue<TreeNode> queue = new LinkedList <>(); queue.add(root); TreeNode pre = root; while (!queue.isEmpty()){ TreeNode cur = queue.poll(); if (pre==null && cur!=null ){ return false ; } if (cur!=null ) { queue.add(cur.left); queue.add(cur.right); } pre = cur; } return true ; }
将一个按照升序排列的有序数组,转换为一棵高度平衡二叉搜索树
本题中,一个高度平衡二叉树是指一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1。
示例:
给定有序数组:[-10 ,-3 ,0 ,5 ,9 ] 一个可能的答案是:[0 ,-3 ,9 ,-10 ,null ,5 ],它可以表示下面这个高度平衡二叉搜索树: 0 / \ -3 9 / / -10 5
解法一
public TreeNode sortedArrayToBST (int [] nums) { return sortedArrayToBST(nums,0 ,nums.length-1 ); } public TreeNode sortedArrayToBST (int [] nums,int left,int right) { if (left>right) { return null ; } int mid=(right-left)/2 +left; TreeNode node=new TreeNode (nums[mid]); node.left=sortedArrayToBST(nums,left,mid-1 ); node.right=sortedArrayToBST(nums,mid+1 ,right); return node; }
这题最开始终止条件写错了,思路是对的,对递归运用的还是不够熟练,终止条件其实只需要想一下极端情况就可以了
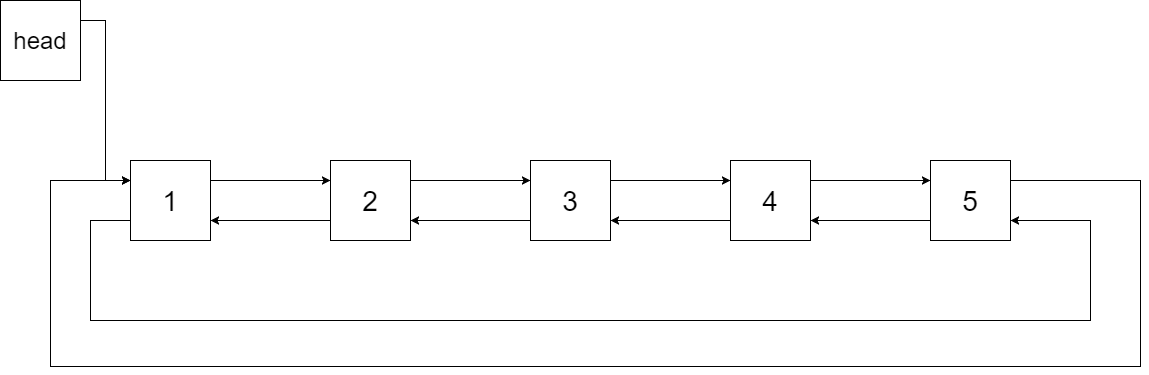
给定一个单链表,其中的元素按升序排序,将其转换为高度平衡的二叉搜索树。
本题中,一个高度平衡二叉树是指一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1。
示例:
给定的有序链表: [-10 , -3 , 0 , 5 , 9 ], 一个可能的答案是:[0 , -3 , 9 , -10 , null , 5 ], 它可以表示下面这个高度平衡二叉搜索树: 0 / \ -3 9 / / -10 5
解法一
BST 不太熟看了下评论写出来的
好久之前写的题了,每日打卡题出了上面的题目,随便做一下这题,发现这题被记录在链表专题中了,移过来下,和上面的一样,只不过找中点的方式不一样(UPDATE: 2020.7.3)
public TreeNode sortedListToBST (ListNode head) { return build(head,null ); } public static TreeNode build (ListNode head,ListNode tail) { if (head==tail){ return null ; } ListNode fast=head,slow=head; while (fast!=tail&&fast.next!=tail){ fast=fast.next.next; slow=slow.next; } TreeNode root=new TreeNode (slow.val); root.left=build(head,slow); root.right=build(slow.next,tail); return root; }
UPDATE: 2020.7.3
func sortedListToBST (head *ListNode) if head == nil { return nil } if head.Next == nil { return &TreeNode{Val : head.Val} } var fast = head var slow = head var pre = head for fast != nil && fast.Next !=nil { fast = fast.Next.Next pre = slow slow = slow.Next } pre.Next = nil root := &TreeNode{Val : slow.Val} root.Left = sortedListToBST(head) root.Right = sortedListToBST(slow.Next) return root }
给定一个二叉搜索树,编写一个函数 kthSmallest 来查找其中第 k 个最小的元素
说明:
示例 1:
输入:root = [3 ,1 ,4 ,null ,2 ], k = 1 3 / \ 1 4 \ 2 输出:1
示例 2:
输入:root = [5 ,3 ,6 ,2 ,4 ,null ,null ,1 ], k = 3 5 / \ 3 6 / \ 2 4 / 1 输出:3
进阶:
解法一
非递归中序遍历
public int kthSmallest (TreeNode root, int k) { Stack<TreeNode> stack=new Stack <>(); TreeNode cur=root; int count=0 ; while (cur!=null || !stack.isEmpty()){ while (cur!=null ){ stack.add(cur); cur=cur.left; } cur=stack.pop(); if (count==k-1 ) { return cur.val; } cur=cur.right; count++; } return -1 ; }
还是利用 BST 中序遍历是升序的性质,在取到第 k 个元素的时候就直接break
解法二
递归的方式,加了两个额外的实例变量其实不太好
public int kthSmallest (TreeNode root, int k) { kthSmallest(root,k); return res; } private int count=0 ;private int res=0 ;public void kthSmall (TreeNode root, int k) { if (root==null ) { return ; } kthSmall(root.left,k); if (count==k-1 ) { res=root.val; return ; } count++; kthSmall(root.right,k); }
如果是第 K 大就交换下遍历顺序就行了
func kthLargest (root *TreeNode, k int ) int { var res = root.Val var count = 0 var dfs func (*TreeNode) dfs = func (root *TreeNode) if root == nil { return } dfs(root.Right) count++ if count == k{ res = root.Val } dfs(root.Left) } dfs(root) return res }
进阶
可以维护一个大根堆,就和最小栈一样,每次对 BST 操作的时候同步操作这个大根堆
给定一个二叉树,找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
例如,给定如下二叉树:root = [3,5,1,6,2,0,8,null,null,7,4]
示例 1:
输入:root = [3 ,5 ,1 ,6 ,2 ,0 ,8 ,null ,null ,7 ,4 ], p = 5 , q = 1 输出:3 解释:节点 5 和节点 1 的最近公共祖先是节点 3 。
示例 2:
输入:root = [3 ,5 ,1 ,6 ,2 ,0 ,8 ,null ,null ,7 ,4 ], p = 5 , q = 4 输出:5 解释:节点 5 和节点 4 的最近公共祖先是节点 5 。因为根据定义最近公共祖先节点可以为节点本身。
说明:
所有节点的值都是唯一的。
p、q 为不同节点且均存在于给定的二叉树中。
解法一
public TreeNode lowestCommonAncestor (TreeNode root, TreeNode p, TreeNode q) { if (root==null || root==p || root==q) return root; TreeNode left=lowestCommonAncestor(root.left,p,q); TreeNode right=lowestCommonAncestor(root.right,p,q); if (left==null ){ return right; }else if (right==null ){ return left; } return root; }
这个函数的功能有三个:给定两个节点 pp 和 qq
如果 pp 和 qq 都存在,则返回它们的公共祖先
如果只存在一个,则返回存在的一个
如果 pp 和 qq 都不存在,则返回 NULL
解法二
2020.4.9 新增解法,利用 Map 记录父节点,然后根据 p,q 倒推就行了
public TreeNode lowestCommonAncestor (TreeNode root, TreeNode p, TreeNode q) { if (root == null || p==root ||q==root) { return root; } Deque<TreeNode> stack=new ArrayDeque <>(); HashMap<Integer,TreeNode> map=new HashMap <>(); map.put(root.val,null ); stack.push(root); while (!stack.isEmpty()){ TreeNode cur=stack.poll(); if (cur.right!=null ){ stack.push(cur.right); map.put(cur.right.val,cur); } if (cur.left!=null ){ stack.push(cur.left); map.put(cur.left.val,cur); } } HashSet<Integer> set=new HashSet <>(); while (p!=null ){ set.add(p.val); p=map.get(p.val); } while (!set.contains(q.val)){ q=map.get(q.val); } return q; }
给定一个二叉树,检查它是否是镜像对称的。
例如,二叉树 [1,2,2,3,4,4,3] 是对称的
但是下面这个 [1,2,2,null,3,null,3] 则不是镜像对称 的:
说明:
如果你可以运用递归和迭代两种方法解决这个问题,会很加分。
解法一
哎,感觉刷题还是得在白天,脑子清醒点,下午就感觉做题老是出问题,一开始题都没看清就开始做
其实一开始是想 BFS 层次遍历然后判断每一层是不是镜像对称的,然后发现有些 case 是过不了的,比如
[1,3,3,2,null,2] 这样的 case
层序遍历判断不出了这样的 case 下面解法四打脸
然后换一种遍历方式,其实一开始就想到了前序遍历,如果是镜像对称的话,前序遍历刚好就是对称的,但是!!!还是有 case 过不了!!!我们再看上面的 case,我们改一改
第192/195 个 case,我惊了,居然还有这种操作!!!实在没办法翻了下解答,发现有位老兄也是这样做的,然后他很巧妙的在每个节点值后面加了一个层数 ,他好像是直接当作字符串添加的,我感觉不太好,改用了数组,最后判断的时候需要保证层数和值都相同才行,完整代码如下
public boolean isSymmetric (TreeNode root) { if (root == null ) { return true ; } List<Integer[]> lis=new ArrayList <>(); preTravle(root,lis,0 ); for (int i=0 ,j=lis.size()-1 ;i<=j;i++,j--) { if (lis.get(i)[0 ]!= lis.get(j)[0 ] || lis.get(j)[1 ]!= lis.get(i)[1 ]) { return false ; } } return true ; } public void preTravle (TreeNode node,List<Integer[]> lis,int k) { if (node!=null ) { preTravle(node.left,lis,k+1 ); Integer[] temp=new Integer [2 ]; temp[0 ]=node.val; temp[1 ]=k; lis.add(temp); preTravle(node.right,lis,k+1 ); } }
解法二
递归的解法,应该算是官解了,一开始也是想用递归写的,没抓住问题的本质,太菜了
public boolean isSymmetric (TreeNode root) { if (root ==null ) { return true ; } return isSymmetric(root.left,root.right); } public boolean isSymmetric (TreeNode t1,TreeNode t2) { if (t1==null && t2==null ) { return true ; } if (t1== null || t2==null ) { return false ; } return t1.val==t2.val && isSymmetric(t1.left,t2.right) && isSymmetric(t1.right,t2.left); }
一棵树是镜像对称,说明左右子树左右对称,所以这个问题就可以转换为,判断左右两颗子树是否是镜像对称的问题
判断两颗树是否成镜像对称的话,其实就和照镜子一样的,如上图,判断左子树和右子树是否成镜像对称,就需要判断** t1 的左子树和 t2 的右子树是否镜像对称,t1 的右子树和 t2 的左子树是否镜像对称**,根据这个就可以写出递归函数,还是挺妙的
解法三
类似于层次遍历,其实就是根据上面的递归方法改来的,核心思想和上面递归的是一样的
public boolean isSymmetric (TreeNode root) { if (root ==null ) { return true ; } Stack<TreeNode> stack=new Stack <>(); stack.push(root.left); stack.push(root.right); while (!stack.isEmpty()){ TreeNode t1=stack.pop(); TreeNode t2=stack.pop(); if (t1==null && t2==null ) { continue ; } if (t1==null ||t2==null || t1.val!=t2.val) { return false ; } stack.push(t1.left); stack.push(t2.right); stack.push(t1.right); stack.push(t2.left); } return true ; }
解法四
前序遍历,其实我一开始也想到了用占位的方式,但是因为之前遍历方式不同,导致没想好在哪里加
public boolean isSymmetric (TreeNode root) { if (root ==null ) { return true ; } Queue<TreeNode> queue=new LinkedList <>(); queue.add(root); while (!queue.isEmpty()){ int count=queue.size(); ArrayList<Integer> lis=new ArrayList <>(); while (count>0 ){ TreeNode node=queue.poll(); if (node.left!=null ) { queue.add(node.left); lis.add(node.left.val); }else { lis.add(-1 ); } if (node.right!=null ) { queue.add(node.right); lis.add(node.right.val); }else { lis.add(-1 ); } count--; } for (int i=0 ,j=lis.size()-1 ;i<=j;i++,j--) { if (lis.get(i)!=lis.get(j)) { return false ; } } } return true ; }
这样的做法明显时间复杂度会之前要高,不仅遍历了整颗树一遍,还对每一层遍历了一遍,一共遍历了两遍
给定一个二叉树,在树的最后一行找到最左边的值。
示例 1:
示例 2:
输入: 1 / \ 2 3 / / \ 4 5 6 / 7 输出: 7
注意: 您可以假设树(即给定的根节点)不为 NULL。
解法一
这种题写一百遍了😂,然而我还是没有 bugfree
public int findBottomLeftValue (TreeNode root) { Queue<TreeNode> queue=new LinkedList <>(); queue.add(root); int res=-1 ; while (!queue.isEmpty()){ int count=queue.size(); int temp=count; while (count>0 ){ TreeNode node=queue.poll(); if (count==temp) { res=node.val; } if (node.left!=null ) { queue.add(node.left); } if (node.right!=null ) { queue.add(node.right); } count--; } } return res; }
解法二
最左边的值,也就是最后一行的第一个元素,dfs 深度优先,深度每增加一次就更新一次 res
public int findBottomLeftValue2 (TreeNode root) { dfs(root,0 ); return res; } int res=-1 ,max=Integer.MIN_VALUE;public void dfs (TreeNode node,int depth) { if (node==null ) return ; if (depth>max) { max=depth; res=node.val; } dfs(node.left,depth+1 ); dfs(node.right,depth+1 ); }
根据一棵树的前序遍历与中序遍历构造二叉树。
注意:
例如,给出
前序遍历 preorder = [3 ,9 ,20 ,15 ,7 ] 中序遍历 inorder = [9 ,3 ,15 ,20 ,7 ]
返回如下的二叉树:
解法一
public TreeNode buildTree (int [] preorder, int [] inorder) { if (preorder==null ) { return null ; } return buildTree(preorder,0 ,preorder.length-1 ,inorder,0 ,inorder.length-1 ); } public TreeNode buildTree (int [] preorder,int preleft,int preright,int [] inorder,int inleft,int inright) { if (preleft>preright || inleft>inright) { return null ; } TreeNode root=new TreeNode (preorder[preleft]); int index=inleft; while (inorder[index] != preorder[preleft]) { index++; } root.left=buildTree(preorder,preleft+1 ,preleft+index-inleft,inorder,inleft,index-1 ); root.right=buildTree(preorder,preleft+index-inleft+1 ,preright,inorder,index+1 ,inright); return root; }
这题核心思想就是利用这几种遍历的性质,文字总是苍白的,看个图吧
这样一看就清晰了,前序遍历左边第一个节点 1 一定是根节点,所以我们首先确定了根节点,然后我们去中序遍历中去找这个根节点(一定有),如上图,我们找到了中间的 1然后再根据中序遍历的性质,我们可以就知道,中序遍历中,这个1 的左边是 1 的左子树,右边是1 的右子树,到这里我们就确定了根节点及其左右子树,剩下的就交给递归去完成了😁,我们只需要对左右子树分别递归该过程就可以得到一颗完整的树了
当然这里值得注意的地方就是下标的变换,要十分注意,自己带入几个值试试
UPDATE(2020.5.22)
var m map [int ]int func buildTree (preorder []int , inorder []int ) n:=len (inorder) m=make (map [int ]int ,n) for i,val:=range inorder{ m[val]=i } return build(preorder,0 ,n-1 ,inorder,0 ,n-1 ) } func build (pre []int ,pl int ,pr int ,in []int ,il int ,ir int ) if pl>pr || il>ir{ return nil } root:=&TreeNode{Val:pre[pl]} idx:=m[pre[pl]] root.Left=build(pre,pl+1 ,pl+idx-il,in,il,idx-1 ) root.Right=build(pre,pl+idx-il+1 ,pr,in,idx+1 ,ir) return root }
根据一棵树的中序遍历与后序遍历构造二叉树。
注意:
例如,给出
中序遍历 inorder = [9 ,3 ,15 ,20 ,7 ] 后序遍历 postorder = [9 ,15 ,7 ,20 ,3 ]
返回如下的二叉树:
解法一
方法同上,只不过是从后往前了
public TreeNode buildTree (int [] inorder, int [] postorder) { if (inorder==null || inorder.length<=0 ) { return null ; } return buildTree(inorder,0 ,inorder.length-1 ,postorder,0 ,postorder.length-1 ); } public TreeNode buildTree (int [] inorder,int inL,int inR, int [] postorder,int pL,int pR) { if (inL>inR || pL>pR) { return null ; } TreeNode root=new TreeNode (postorder[pR]); int index=inL; while (inorder[index]!=postorder[pR]){ index++; } root.left=buildTree(inorder,inL,index-1 ,postorder,pL,pL+index-inL-1 ); root.right=buildTree(inorder,index+1 ,inR,postorder,pL+index-inL,pR-1 ); return root; }
和上面一样没啥好说的
解法二
上面两种解法提交后效率都不高,这里去中序遍历中找根节点的操作其实可以用 Hash 表代替
HashMap<Integer,Integer> map=new HashMap <>(); public TreeNode buildTree (int [] inorder, int [] postorder) { if (inorder==null || inorder.length<=0 ) { return null ; } for (int i=0 ;i<inorder.length;i++) { map.put(inorder[i],i); } return buildTree(inorder,0 ,inorder.length-1 ,postorder,0 ,postorder.length-1 ); } public TreeNode buildTree (int [] inorder,int inL,int inR, int [] postorder,int pL,int pR) { if (inL>inR || pL>pR) { return null ; } TreeNode root=new TreeNode (postorder[pR]); int index=map.get(postorder[pR]); root.left=buildTree(inorder,inL,index-1 ,postorder,pL,pL+index-inL-1 ); root.right=buildTree(inorder,index+1 ,inR,postorder,pL+index-inL,pR-1 ); return root; }
返回与给定的前序和后序遍历匹配的任何二叉树。
pre 和 post 遍历中的值是不同的正整数。
示例:
输入:pre = [1 ,2 ,4 ,5 ,3 ,6 ,7 ], post = [4 ,5 ,2 ,6 ,7 ,3 ,1 ] 输出:[1 ,2 ,3 ,4 ,5 ,6 ,7 ]
提示:
1 <= pre.length == post.length <= 30pre[] 和 post[] 都是 1, 2, …, pre.length 的排列每个输入保证至少有一个答案。如果有多个答案,可以返回其中一个。
解法一
和上面的有一点点区别
HashMap<Integer,Integer> map=new HashMap <>(); public TreeNode constructFromPrePost (int [] pre, int [] post) { for (int i=0 ;i<post.length;i++) { map.put(post[i],i); } return constructFromPrePost(pre,0 ,pre.length-1 ,post,0 ,post.length-1 ); } public TreeNode constructFromPrePost (int [] pre,int preL,int preR,int [] post,int postL,int postR) { if (preL>preR || postL>preR) { return null ; } TreeNode root=new TreeNode (pre[preL]); if (preL==preR) { return root; } int postIndex=map.get(pre[preL+1 ]); int len=postIndex-postL; root.left=constructFromPrePost(pre,preL+1 ,preL+1 +len,post,postL,postIndex); root.right=constructFromPrePost(pre,preL+2 +len,preR,post,postIndex+1 ,postR-1 ); return root; }
还是这张图,前序的第一个是根节点,后序的最后一个是根节点,而我们要找的是左右子树的分界线,这里没有中序遍历,乍一看似乎不好确定,其实不然,注意观察前序的第二个节点,也就是左子树的根节点,比如上面的 2,对应到后序遍历中其实正好就可以作为左子树的分界线,这样一来就和上面一样了,所以这里的关键就是找到一个划分点
🔔 有一点需要注意,题目说了这题的结果可能是不唯一的,数据结构的课程里面也讲过,仅凭前序和后序是无法确定一颗二叉树的,但是一定么?
并不一定,我们题目的 case 就是个反例,它就可以通过前序和后序唯一的确定这颗二叉树,那什么时候可以确定,什么时候无法确定呢?
无法确定的例子好说,【1,2】,【2,1】这个就无法确定
但是如果是这样的【1,2,3】【2,3,1】这种就可以唯一的确定
归纳总结一下,可以发现,如果这颗二叉树每个节点的度都是 0 或者 2 那么他就可以通过前序和后序确定,反之就不一定了,因为你只有一个子节点那么就无法确定这个节点是左节点还是右节点,如果没有或者两个都有那么就可以确定了(根据顺序确定,前面的是左后面的是右,但是你只有一个我就不知道是左还是右了)
给定一个二叉树,原地将它展开为链表。
例如,给定二叉树
将其展开为:
题目没抄错,就是这样的,确实题目没有说明按照什么方式展开,但是看 case 能猜到是前序遍历的方式展开(靠猜的?)
解法一
前序遍历,递归的解法,用一个全局变量保存链表的结尾,每次将节点添加到 last 的后面
TreeNode last=null ; public void flatten (TreeNode root) { if (root==null ) { return ; } if (last!=null ) { last.left=null ; last.right=root; } last=root; TreeNode right=root.right; flatten(root.left); flatten(right); }
需要注意的地方就是需要保存右子树,因为前面的操作将左子树添加到根节点右子树的时候,会导致原本的右子树丢失
非递归的写法
public void flatten (TreeNode root) { if (root==null ) return ; TreeNode last=null ; Deque<TreeNode> stack=new ArrayDeque <>(); stack.push(root); while (!stack.isEmpty()){ TreeNode cur=stack.pop(); if (last!=null ){ last.right=cur; last.left=null ; } last=cur; if (cur.right!=null ){ stack.push(cur.right); } if (cur.left!=null ){ stack.push(cur.left); } } }
解法二
变形的后序遍历,递归解法
TreeNode pre=null ; public void flatten (TreeNode root) { if (root==null ) { return ; } flatten(root.right); flatten(root.left); root.right=pre; root.left=null ; pre=root; }
相比前面的解法,为了不丢失右子树,先遍历右子树,再遍历左子树,整个序列就是6 5 4 3 2 1 我们只需要将每个节点的 right 指向前一个节点就 ok 了
解法三
迭代,我觉得这种解法挺秀,而且是完全的 in-place,但是时间复杂度会高一些,每个元素不只遍历一次
public void flatten (TreeNode root) { TreeNode mRight=null ; while (root!=null ){ if (root.left!=null ) { mRight=root.left; while (mRight.right!=null ){ mRight=mRight.right; } mRight.right=root.right; root.right=root.left; root.left=null ; } root=root.right; } }
画个图就是这样
输入一棵二叉搜索树,将该二叉搜索树转换成一个排序的循环双向链表。要求不能创建任何新的节点,只能调整树中节点指针的指向。
为了让您更好地理解问题,以下面的二叉搜索树为例:
我们希望将这个二叉搜索树转化为双向循环链表。链表中的每个节点都有一个前驱和后继指针。对于双向循环链表,第一个节点的前驱是最后一个节点,最后一个节点的后继是第一个节点。
下图展示了上面的二叉搜索树转化成的链表。“head” 表示指向链表中有最小元素的节点。
解法一
开始还以为挺难搞,一遍就写出来了😁比上一题简单
public Node treeToDoublyList (Node root) { if (root==null ) return root; dfs(root); head.left=lastNode; lastNode.right=head; return head; } Node lastNode,head=null ; public void dfs (Node root) { if (root==null ) return ; dfs(root.left); if (lastNode==null ){ head=lastNode=root; }else { root.left=lastNode; lastNode.right=root; lastNode=root; } dfs(root.right); }
给定一个完美二叉树 ,其所有叶子节点都在同一层,每个父节点都有两个子节点。二叉树定义如下:
struct Node { int val; Node *left; Node *right; Node *next; }
填充它的每个 next 指针,让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点,则将 next 指针设置为 NULL
初始状态下,所有 next 指针都被设置为 NULL
解法一
开始没做出来,菜!!!然后特意留到今天总结,又在 web 上提交了一遍
public Node connect (Node root) { if (root ==null ||root.left==null ) { return root; } root.left.next=root.right; if (root.next!=null ) { root.right.next=root.next.left; } connect(root.left); connect(root.right); return root; }
解法二
这个解法梳理还是很清奇的,类似拉拉链的过程
public Node connect (Node root) { if (root ==null ||root.left==null ) { return root; } Node left=root.left; Node right=root.right; while (left!=null ){ left.next=right; left=left.right; right=right.left; } connect(root.left); connect(root.right); return root; }
还有一个很直白的层序遍历的方法,这里就不写了
给定一个二叉树
struct Node { int val; Node *left; Node *right; Node *next; }
填充它的每个 next 指针,让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点,则将 next 指针设置为 NULL。
初始状态下,所有 next 指针都被设置为 NULL。
进阶:
你只能使用常量级额外空间。
使用递归解题也符合要求,本题中递归程序占用的栈空间不算做额外的空间复杂度。
示例:
输入:root = [1 ,2 ,3 ,4 ,5 ,null ,7 ] 输出:[1 ,#,2 ,3 ,#,4 ,5 ,7 ,#] 解释:给定二叉树如图 A 所示,你的函数应该填充它的每个 next 指针,以指向其下一个右侧节点,如图 B 所示。
提示:
树中的节点数小于 6000
-100 <= node.val <= 100
解法一
题目要求的 O(1) 空间,参考了大佬的解法,模拟层序遍历,着实是很巧妙,代码简洁清晰,值得细细品味
public Node connect (Node root) { Node dummyNode=new Node (-1 ); Node cur=root; while (cur!=null ){ dummyNode.next=null ; Node tail=dummyNode; while (cur!=null ){ if (cur.left!=null ){ tail.next=cur.left; tail=tail.next; } if (cur.right!=null ){ tail.next=cur.right; tail=tail.next; } cur=cur.next; } cur=dummyNode.next; } return root; }
给定一个二叉搜索树的根节点 root 和一个值 key,删除二叉搜索树中的 key 对应的节点,并保证二叉搜索树的性质不变。返回二叉搜索树(有可能被更新)的根节点的引用。
一般来说,删除节点可分为两个步骤:
首先找到需要删除的节点;
如果找到了,删除它。
说明: 要求算法时间复杂度为 O(h),h 为树的高度。
示例:
root = [5 ,3 ,6 ,2 ,4 ,null ,7 ] key = 3 5 / \ 3 6 / \ \ 2 4 7 给定需要删除的节点值是 3 ,所以我们首先找到 3 这个节点,然后删除它。 一个正确的答案是 [5 ,4 ,6 ,2 ,null ,null ,7 ], 如下图所示。 5 / \ 4 6 / \ 2 7 另一个正确答案是 [5 ,2 ,6 ,null ,4 ,null ,7 ]。 5 / \ 2 6 \ \ 4 7
解法一
更多解释看另一篇 二叉搜索树
public TreeNode deleteNode (TreeNode root, int key) { if (root ==null ) { return null ; } if (root.val>key) { root.left=deleteNode(root.left,key); }else if (root.val<key) { root.right=deleteNode(root.right,key); }else { if (root.left==null ) { return root.right; } if (root.right==null ) { return root.left; } TreeNode delNode=root; root=getMin(root.right); root.right=deleteMin(delNode.right); root.left=delNode.left; } return root; } public TreeNode deleteMin (TreeNode node) { if (node.left==null ) { return node.right; } node.left=deleteMin(node.left); return node; } public TreeNode getMin (TreeNode node) { if (node.left==null ) { return node; } return getMin(node.left); }
给定二叉搜索树(BST)的根节点和要插入树中的值,将值插入二叉搜索树。 返回插入后二叉搜索树的根节点。 保证原始二叉搜索树中不存在新值。
注意,可能存在多种有效的插入方式,只要树在插入后仍保持为二叉搜索树即可。 你可以返回任意有效的结果。
例如,
给定二叉搜索树:
你可以返回这个二叉搜索树:
或者这个树也是有效的:
解法一
public TreeNode insertIntoBST (TreeNode root, int val) { if (root==null ) { return new TreeNode (val); } if (root.val>val) { root.left=insertIntoBST(root.left,val); }else if (root.val<val) { root.right=insertIntoBST(root.right,val); } return root; }
没啥好说的,看代码就懂了
给定一个二叉树,编写一个函数来获取这个树的最大宽度。树的宽度是所有层中的最大宽度。这个二叉树与满二叉树(full binary tree)结构相同,但一些节点为空。
每一层的宽度被定义为两个端点(该层最左和最右的非空节点,两端点间的 null 节点也计入长度)之间的长度。
Example 1:
Input: 1 / \ 3 2 / \ \ 5 3 9 Output: 4 Explanation: The maximum width existing in the third level with the length 4 (5 ,3 ,null ,9 ).
Example 2:
Input: 1 / 3 / \ 5 3 Output: 2 Explanation: The maximum width existing in the third level with the length 2 (5 ,3 ).
Example 3:
Input: 1 / \ 3 2 / 5 Output: 2 Explanation: The maximum width existing in the second level with the length 2 (3 ,2 ).
Example 4:
Input: 1 / \ 3 2 / \ 5 9 / \ 6 7 Output: 8 Explanation:The maximum width existing in the fourth level with the length 8 (6 ,null ,null ,null ,null ,null ,null ,7 ).
Note: Answer will in the range of 32-bit signed integer.
解法一
一开始居然没想到,哎😐还是菜啊
public int widthOfBinaryTree (TreeNode root) { if (root==null ) { return 0 ; } Queue<TreeNode> queue=new LinkedList <>(); LinkedList<Integer> idxs=new LinkedList <>(); int max=1 ; idxs.add(1 ); queue.add(root); while (!queue.isEmpty()){ int size=queue.size(); while (size>0 ){ TreeNode top=queue.poll(); int index=idxs.removeFirst(); if (top.left!=null ) { queue.add(top.left); idxs.add(index*2 ); } if (top.right!=null ) { queue.add(top.right); idxs.add(index*2 +1 ); } size--; } if (idxs.size()!=0 ) { max=Math.max(idxs.getLast()-idxs.getFirst()+1 ,max); } } return max; }
还是层次遍历的思路,不过需要额外添加一个索引列表,用来记录每个节点对应在完全二叉树中的索引 ,这个索引值完全可以根据上一层父节点的索引的到,我们初始化定义根节点的 index 为 1,然后进行层次遍历记录每一层的每个节点的 index 就 ok,当遍历完一层之后统计列表最左和最右两个节点之差,这个值就是当前层的宽度,最后求个最大值就 ok 了,很可惜,看了答案才知道
解法二
递归版本
public int widthOfBinaryTree (TreeNode root) { if (root==null ) { return 0 ; } dfs(root,0 ,0 ,new LinkedList <>()); return max; } int max=1 ;public void dfs (TreeNode node,int depth,int index,List<Integer> leftIdxs) { if (node==null ) { return ; } if (depth>=leftIdxs.size()) { leftIdxs.add(index); } max=Math.max(index-leftIdxs.get(depth)+1 ,max); dfs(node.left,depth+1 ,index*2 ,leftIdxs); dfs(node.right,depth+1 ,index*2 +1 ,leftIdxs); }
这个版本在空间复杂度可能会低一点,list 中只存每个层最左的节点,当深度大于等于 list 的长度时候说明当前节点一定是新一层的最左节点,这个时候添加进去就 ok,然后求每个节点和当前层最左的节点 index 差值就最后更新最大值就 ok,这个解法还是没有那么自然,还是上面的 BFS 好理解一点
给定一个非空特殊的二叉树,每个节点都是正数,并且每个节点的子节点数量只能为 2 或 0。如果一个节点有两个子节点的话,那么这个节点的值不大于它的子节点的值。
给出这样的一个二叉树,你需要输出所有节点中的第二小的值。如果第二小的值不存在的话,输出 -1 。
示例 1:
输入: 2 / \ 2 5 / \ 5 7 输出:5 说明:最小的值是 2 ,第二小的值是 5 。
示例 2:
输入: 2 / \ 2 2 输出:-1 说明:最小的值是 2 , 但是不存在第二小的值。
解法一
var INT_MAX = int (^uint (0 ) >> 1 )func findSecondMinimumValue (root *TreeNode) int { res := dfs(root) if res == INT_MAX { return -1 } return res } func dfs (root *TreeNode) int { if root == nil || root.Left == nil { return INT_MAX } if root.Val != root.Left.Val && root.Val != root.Right.Val { return min(root.Left.Val, root.Right.Val) } if root.Val == root.Left.Val && root.Val == root.Right.Val { return min(dfs(root.Left), dfs(root.Right)) } if root.Val == root.Left.Val { return min(dfs(root.Left), root.Right.Val) } return min(dfs(root.Right), root.Left.Val) } func min (a, b int ) int { if a > b { return b } return a }
给定二叉搜索树的根结点 root,返回 L 和 R(含)之间的所有结点的值的和。
二叉搜索树保证具有唯一的值。
示例 1:
输入:root = [10 ,5 ,15 ,3 ,7 ,null ,18 ], L = 7 , R = 15 输出:32
示例 2:
输入:root = [10 ,5 ,15 ,3 ,7 ,13 ,18 ,1 ,null ,6 ], L = 6 , R = 10 输出:23
提示:
树中的结点数量最多为 10000 个。
最终的答案保证小于 2^31
解法一
还行,这题反应过来了,中序遍历
private int sum=0 ;public int rangeSumBST (TreeNode root, int L, int R) { preorder(root,L,R); return sum; } public void preorder (TreeNode root, int L, int R) { if (root==null ) { return ; } rangeSumBST(root.left,L,R); if (root.val>=L && root.val<=R) { sum+=root.val; } rangeSumBST(root.right,L,R); }
给定两个二叉树,想象当你将它们中的一个覆盖到另一个上时,两个二叉树的一些节点便会重叠。
你需要将他们合并为一个新的二叉树。合并的规则是如果两个节点重叠,那么将他们的值相加作为节点合并后的新值,否则不为 NULL 的节点将直接作为新二叉树的节点。
示例 1:
输入: Tree 1 Tree 2 1 2 / \ / \ 3 2 1 3 / \ \ 5 4 7 输出: 合并后的树: 3 / \ 4 5 / \ \ 5 4 7
注意: 合并必须从两个树的根节点开始。
解法一
public TreeNode mergeTrees (TreeNode t1, TreeNode t2) { if (t2==null ) { return t1; } if (t1==null ) { return t2; } t1.val+=t2.val; t1.left=mergeTrees(t1.left,t2.left); t1.right=mergeTrees(t1.right,t2.right); return t1; }
给定一个所有节点为非负值的二叉搜索树,求树中任意两节点的差的绝对值的最小值。
示例 :
输入: 1 \ 3 / 2 输出: 1 解释: 最小绝对差为 1 ,其中 2 和 1 的差的绝对值为 1 (或者 2 和 3 )。
注意: 树中至少有 2 个节点。
解法一
很可惜,这题还 WA 了一次。
public int getMinimumDifference (TreeNode root) { Stack<TreeNode> stack=new Stack <>(); TreeNode cur=root; int diff=Integer.MAX_VALUE,last=-1 ; while (!stack.isEmpty() || cur!=null ){ while (cur!=null ){ stack.push(cur); cur=cur.left; } cur=stack.pop(); if (last!=-1 ) { diff=Math.min(diff,Math.abs(last-cur.val)); } last=cur.val; cur=cur.right; } return diff; }
解法二
递归的方式
private int diff = Integer.MAX_VALUE;private int last = -1 ;public int getMinimumDifference (TreeNode root) { inorder(root); return diff; } public void inorder (TreeNode root) { if (root==null ) { return ; } inorder(root.left); diff = last==-1 ?diff:Math.min(diff,Math.abs(last-root.val)); last = root.val; inorder(root.right); }
Difficulty: 简单
给定一个有相同值的二叉搜索树(BST),找出 BST 中的所有众数(出现频率最高的元素)。
假定 BST 有如下定义:
结点左子树中所含结点的值小于等于当前结点的值
结点右子树中所含结点的值大于等于当前结点的值
左子树和右子树都是二叉搜索树
例如:[1,null,2,2],
返回 [2].
提示 :如果众数超过 1 个,不需考虑输出顺序
进阶: 你可以不使用额外的空间吗?(假设由递归产生的隐式调用栈的开销不被计算在内)
解法一
之前忘了记录了,中序遍历统计答案就 ok,但是非要严格的 O(1) 就需要使用 Morris 遍历(不会
func findMode (root *TreeNode) int { var dfs func (root *TreeNode) var prev *TreeNode var count, max = 0 , 0 var res []int dfs = func (root *TreeNode) if root == nil { return } dfs(root.Left) if prev == nil || prev.Val == root.Val { count++ } else { count = 1 } if count == max { res = append (res, root.Val) } if count > max { res = []int {} res = append (res, root.Val) max = count } prev = root dfs(root.Right) } dfs(root)
您需要在二叉树的每一行中找到最大的值。
示例:
输入: 1 / \ 3 2 / \ \ 5 3 9 输出:[1 , 3 , 9 ]
解法一
娱乐题
public List<Integer> largestValues (TreeNode root) { List<Integer> res=new ArrayList <>(); dfs(root,res,0 ); return res; } public void dfs (TreeNode node,List<Integer> list,int level) { if (node==null ) { return ; } if (level>=list.size()) { list.add(node.val); } if (node.val>list.get(level)){ list.set(level,node.val); } dfs(node.left,list,level+1 ); dfs(node.right,list,level+1 ); }
实现一个二叉搜索树迭代器。你将使用二叉搜索树的根节点初始化迭代器。
调用 next() 将返回二叉搜索树中的下一个最小的数。
示例:
BSTIterator iterator = new BSTIterator (root);iterator.next(); iterator.next(); iterator.hasNext(); iterator.next(); iterator.hasNext(); iterator.next(); iterator.hasNext(); iterator.next(); iterator.hasNext();
提示:
next() 和 hasNext() 操作的时间复杂度是 O(1),并使用 O(h) 内存,其中 h 是树的高度。
你可以假设 next() 调用总是有效的,也就是说,当调用 next() 时,BST 中至少存在一个下一个最小的数。
解法一
注意这题空间复杂度要求是O(h) ,并不是憨憨题
Stack<TreeNode> stack=new Stack <>(); public BSTIterator (TreeNode root) { pushLeft(root); } public int next () { TreeNode node=stack.pop(); if (node.right!=null ) { pushLeft(node.right); } return node.val; } public boolean hasNext () { return !stack.isEmpty(); } public void pushLeft (TreeNode node) { while (node!=null ){ stack.add(node); node=node.left; } }
我们可以用一个 stack 存储 BST 的左链,当取最小值就从 stack 中直接取,如果取出来的 node 还有右子树就将右子树的左链也添加进来,是不是有点熟悉?其实就是中序遍历的过程
给定一个整数 n,生成所有由 1 … n 为节点所组成的二叉搜索树 。
示例:
输入:3 输出: [ [1 ,null ,3 ,2 ], [3 ,2 ,null ,1 ], [3 ,1 ,null ,null ,2 ], [2 ,1 ,3 ], [1 ,null ,2 ,null ,3 ] ] 解释: 以上的输出对应以下 5 种不同结构的二叉搜索树: 1 3 3 2 1 \ / / / \ \ 3 2 1 1 3 2 / / \ \ 2 1 2 3
解法一
public List<TreeNode> generateTrees (int n) { if (n<=0 ){ return new ArrayList <>(); } return generateTrees(1 ,n); } public List<TreeNode> generateTrees (int start,int end) { List<TreeNode> res=new ArrayList <>(); if (start>end) { res.add(null ); return res; } for (int i=start;i<=end;i++) { List<TreeNode> left=generateTrees(start,i-1 ); List<TreeNode> right=generateTrees(i+1 ,end); for (TreeNode l:left) { for (TreeNode r:right) { TreeNode currentNode=new TreeNode (i); currentNode.left=l; currentNode.right=r; res.add(currentNode); } } } return res; }
很久之前做过的题,今天又拿出来看看,其实属于分治思路
给定一个二叉搜索树(Binary Search Tree),把它转换成为累加树(Greater Tree),使得每个节点的值是原来的节点值加上所有大于它的节点值之和。
例如:
输入:二叉搜索树: 5 / \ 2 13 输出:转换为累加树: 18 / \ 20 13
解法一
这里我想先上一个错误的解法
public TreeNode convertBST (TreeNode root) { if (root==null ) { return new TreeNode (0 ); } if (root.left==null && root.right==null ) { return root; } root.val+= convertBST(root.right).val; convertBST(root.left).val+=root.val; return root; }
忽略返回值的部分,乍一看好像是对的😂,其实问题大了,首先是左边的值算的不对,因为是 DFS 会从最左边开始算,都只加了他的父节点原始的值,而父节点的累加值还没有算出来,其次有些情况是算不出来的比如左子树的某一个右节点你就算不出来
解法二
其实一开始就知道可以直接中序遍历做,只是想玩一些其他的方法,可惜没搞出来😂
public TreeNode convertBST (TreeNode root) { dfs(root); return root; } private int sum=0 ;public void dfs (TreeNode root) { if (root==null ) { return ; } dfs(root.right); sum+=root.val; root.val=sum; dfs(root.left); }
这里需要注意的就是要翻过来遍历,从大到小,因为它求的是比它大的节点的值
给出二叉树的根,找出出现次数最多的子树元素和。一个结点的子树元素和定义为以该结点为根的二叉树上所有结点的元素之和(包括结点本身)。然后求出出现次数最多的子树元素和。如果有多个元素出现的次数相同,返回所有出现次数最多的元素(不限顺序)。
示例 1
输入: 5 / \ 2 -3 返回 [2 , -3 , 4 ],所有的值均只出现一次,以任意顺序返回所有值。
示例 2
输入: 5 / \ 2 -5 返回 [2 ],只有 2 出现两次,-5 只出现 1 次。
解法一
左子树和+右子树和,HashMap 记录出现的次数,记录最大值然后取出出现次数最多的
private Map<Integer,Integer> map = new HashMap <>();private int maxCount=0 ;public int [] findFrequentTreeSum(TreeNode root) { if (root ==null ) { return new int []{}; } dfs(root); List<Integer> res=new ArrayList <>(); map.keySet().stream().filter(val->map.get(val)==maxCount).forEach(res::add); return res.stream().mapToInt(Integer::valueOf).toArray(); } public int dfs (TreeNode root) { if (root==null ) { return 0 ; } int value=root.val+dfs(root.right)+dfs(root.left); map.put(value,map.getOrDefault(value,0 )+1 ); maxCount=Math.max(maxCount,map.get(value)); return value; }
写法是基于 Lambda 的,函数式写起来真的舒服
你需要采用前序遍历的方式,将一个二叉树转换成一个由括号和整数组成的字符串。
空节点则用一对空括号 “()” 表示。而且你需要省略所有不影响字符串与原始二叉树之间的一对一映射关系的空括号对。
示例 1:
输入:二叉树:[1 ,2 ,3 ,4 ] 1 / \ 2 3 / 4 输出:"1(2(4))(3)" 解释:原本将是“1 (2 (4 )())(3 ())”, 在你省略所有不必要的空括号对之后, 它将是“1 (2 (4 ))(3 )”。
示例 2:
输入:二叉树:[1 ,2 ,3 ,null ,4 ] 1 / \ 2 3 \ 4 输出:"1(2()(4))(3)" 解释:和第一个示例相似, 除了我们不能省略第一个对括号来中断输入和输出之间的一对一映射关系。
解法一
public String tree2str (TreeNode t) { StringBuilder s=new StringBuilder (); dfs(t,s); return s.toString(); } public void dfs (TreeNode node,StringBuilder s) { if (node==null ) { return ; } s.append(node.val); if (node.left==null && node.right==null ){ return ; } s.append("(" ); dfs(node.left,s); s.append(")" ); if (node.right==null ) { return ; } s.append("(" ); dfs(node.right,s); s.append(")" ); }
没啥好说的,搞清楚题目意思然后注意递归的几个出口就行了
给你一棵二叉树,请你返回满足以下条件的所有节点的值之和:
该节点的祖父节点的值为偶数。(一个节点的祖父节点是指该节点的父节点的父节点。)
示例:
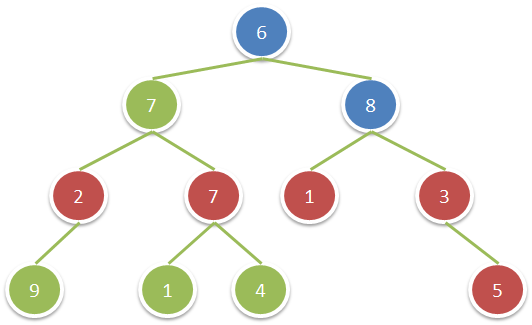
输入:root = [6 ,7 ,8 ,2 ,7 ,1 ,3 ,9 ,null ,1 ,4 ,null ,null ,null ,5 ] 输出:18 解释:图中红色节点的祖父节点的值为偶数,蓝色节点为这些红色节点的祖父节点。
提示:
树中节点的数目在 1 到 10^4 之间。
每个节点的值在 1 到 100 之间。
解法一
好像是 170 前一天的双周赛的第 3 题,还是很直白的题,遍历的时候带上它的 father 的值和 grandfather 的值带到下一层,然后判断就可以了
public int sumEvenGrandparent (TreeNode root) { return dfs(root,-1 ,-1 ); } public int dfs (TreeNode node,int fa,int ga) { if (node==null ) { return 0 ; } int sum=0 ; if (fa!=-1 && ga!=-1 && ga%2 ==0 ) { sum+=node.val; } sum+=dfs(node.left,node.val,fa); sum+=dfs(node.right,node.val,fa); return sum; }
给定二叉树的根节点 root,找出存在于不同节点 A 和 B 之间的最大值 V,其中 V = |A.val - B.val|,且 A 是 B 的祖先。
(如果 A 的任何子节点之一为 B,或者 A 的任何子节点是 B 的祖先,那么我们认为 A 是 B 的祖先)
示例:
输入:[8 ,3 ,10 ,1 ,6 ,null ,14 ,null ,null ,4 ,7 ,13 ] 输出:7 解释: 我们有大量的节点与其祖先的差值,其中一些如下: |8 - 3 | = 5 |3 - 7 | = 4 |8 - 1 | = 7 |10 - 13 | = 3 在所有可能的差值中,最大值 7 由 |8 - 1 | = 7 得出。
提示:
树中的节点数在 2 到 5000 之间。
每个节点的值介于 0 到 100000 之间。
解法一
水题,维护每条路径上的最值,然后统计最大差就行了
func maxAncestorDiff (root *TreeNode) int { var res = 0 dfs(root, 1 <<30 , -1 >>30 , &res) return res } func dfs (root *TreeNode, min, max int , res *int ) if root == nil { return } min = fmin(min, root.Val) max = fmax(max, root.Val) *res = fmax(max-min, *res) dfs(root.Left, min, max, res) dfs(root.Right, min, max, res) } func fmin (a, b int ) int { if a < b { return a } return b } func fmax (a, b int ) int { if a > b { return a } return b }
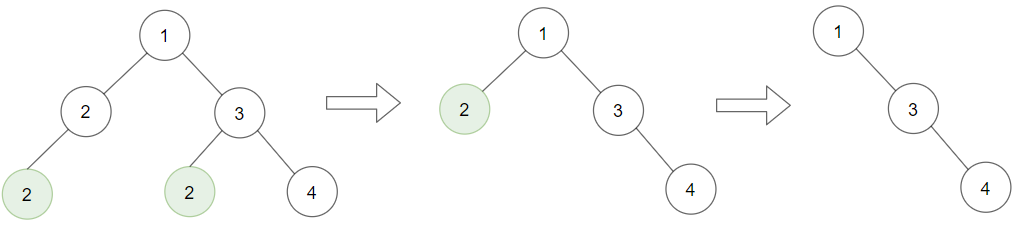
给你一棵以 root 为根的二叉树和一个整数 target ,请你删除所有值为 target 的 叶子节点 。
注意,一旦删除值为 target 的叶子节点,它的父节点就可能变成叶子节点;如果新叶子节点的值恰好也是 target ,那么这个节点也应该被删除。
也就是说,你需要重复此过程直到不能继续删除。
示例 1:
输入:root = [1 ,2 ,3 ,2 ,null ,2 ,4 ], target = 2 输出:[1 ,null ,3 ,null ,4 ] 解释: 上面左边的图中,绿色节点为叶子节点,且它们的值与 target 相同(同为 2 ),它们会被删除,得到中间的图。 有一个新的节点变成了叶子节点且它的值与 target 相同,所以将再次进行删除,从而得到最右边的图。
示例 2:
输入:root = [1 ,3 ,3 ,3 ,2 ], target = 3 输出:[1 ,3 ,null ,null ,2 ]
示例 3:
输入:root = [1 ,2 ,null ,2 ,null ,2 ], target = 2 输出:[1 ] 解释:每一步都删除一个绿色的叶子节点(值为 2 )。
提示:
1 <= target <= 1000每一棵树最多有 3000 个节点。
每一个节点值的范围是 [1, 1000] 。
解法一
某次周赛的第三题
public TreeNode removeLeafNodes (TreeNode root, int target) { return delete(root,target); } public TreeNode delete (TreeNode root,int target) { if (root==null ) { return null ; } root.left=delete(root.left,target); root.right=delete(root.right,target); if (root.left==null && root.right==null && root.val==target) { return null ; } return root; }
搞了半天。一开始写的时候写的前序遍历的方式,先删除自己然后再去删除左右孩子,然后在如何判断是否有叶子节点上卡了半天,最后写了个 for3000 的循环过的。好菜啊,只要交换一下顺序变成后序遍历的方式,先删除左右子节点,然后再回头删除自己的就可以一直删了。
给你 root1 和 root2 这两棵二叉搜索树。
请你返回一个列表,其中包含 两棵树 中的所有整数并按 升序 排序。.
示例 1:
输入:root1 = [2 ,1 ,4 ], root2 = [1 ,0 ,3 ] 输出:[0 ,1 ,1 ,2 ,3 ,4 ]
示例 2:
输入:root1 = [0 ,-10 ,10 ], root2 = [5 ,1 ,7 ,0 ,2 ] 输出:[-10 ,0 ,0 ,1 ,2 ,5 ,7 ,10 ]
示例 3:
输入:root1 = [], root2 = [5 ,1 ,7 ,0 ,2 ] 输出:[0 ,1 ,2 ,5 ,7 ]
示例 4:
输入:root1 = [0 ,-10 ,10 ], root2 = [] 输出:[-10 ,0 ,10 ]
解法一
某次周赛的题,大水题,白板回忆写出了中序的非递归 haha,感觉忘不了了
public List<Integer> getAllElements (TreeNode root1, TreeNode root2) { return megerList(inorder(root1),inorder(root2)); } public List<Integer> inorder (TreeNode root) { List<Integer> res=new ArrayList <>(); Stack<TreeNode> stack=new Stack <>(); TreeNode cur=root; while (!stack.isEmpty() || cur!=null ){ while (cur!=null ){ stack.add(cur); cur=cur.left; } cur=stack.pop(); res.add(cur.val); cur=cur.right; } return res; } public List<Integer> megerList (List<Integer> list1,List<Integer> list2) { List<Integer> res=new ArrayList <>(); int index1=0 ,index2=0 ; while (index1<list1.size() && index2<list2.size()){ res.add(list1.get(index1)<list2.get(index2)?list1.get(index1++):list2.get(index2++)); } while (index1<list1.size()){ res.add(list1.get(index1++)); } while (index2<list2.size()){ res.add(list2.get(index2++)); } return res; } public List<Integer> megerList (List<Integer> list1,int index1,List<Integer> list2,int index2) { List<Integer> res=new ArrayList <>(); if (index1==list1.size()) { for (int i=index2;i<list2.size();i++) { res.add(list2.get(i)); } return res; } if (index2==list2.size()) { for (int i=index1;i<list1.size();i++) { res.add(list1.get(i)); } return res; } if (list1.get(index1)<list2.get(index2)) { res.add(list1.get(index1)); res.addAll(megerList(list1,index1+1 ,list2,index2)); }else { res.add(list2.get(index2)); res.addAll(megerList(list1,index1,list2,index2+1 )); } return res; }
给你一棵二叉树,它的根为 root 。请你删除 1 条边,使二叉树分裂成两棵子树,且它们子树和的乘积尽可能大。
由于答案可能会很大,请你将结果对 10^9 + 7 取模后再返回。
示例 1:
输入:root = [1 ,2 ,3 ,4 ,5 ,6 ] 输出:110 解释:删除红色的边,得到 2 棵子树,和分别为 11 和 10 。它们的乘积是 110 (11 *10 )
示例 2:
输入:root = [1 ,null ,2 ,3 ,4 ,null ,null ,5 ,6 ] 输出:90 解释:移除红色的边,得到 2 棵子树,和分别是 15 和 6 。它们的乘积为 90 (15 *6 )
解法一
174 周赛的第三题,当时比赛 TLE 了。写了个很蠢的算法
private long mod=1000000007 ;public int maxProduct (TreeNode root) { Stack<TreeNode> stack=new Stack <>(); TreeNode cur=root; long sumAll=sum(root); while (!stack.isEmpty() || cur!=null ){ TreeNode temp=null ; long s=0L ; while (cur!=null ){ temp=cur.left; cur.left=null ; long r=sum(root); s=r*(sumAll-r); max=Math.max(s,max); cur.left=temp; stack.add(cur); cur=cur.left; } cur=stack.pop(); temp=cur.right; cur.right=null ; long r=sum(root); s=r*(sumAll-r); max=Math.max(s,max); cur.right=temp; cur=cur.right; } return (int )(max%mod); } private long max=-1 ;public long sum (TreeNode root) { if (root==null ) { return 0 ; } return root.val+sum(root.left)+sum(root.right); }
我居然真的去删除节点去了。导致后面都没办法对 sum 做记忆化,太菜了啊
解法二
能 AC 但是效率感人
private long mod=1000000007 ;private long sumAll=0 ;private long max=-1 ;public int maxProduct (TreeNode root) { sumAll=sum(root); dfs(root); return (int )(max%mod); } public void dfs (TreeNode root) { if (root==null ) { return ; } long temp=sum(root); max=Math.max(max,temp*(sumAll-temp)); dfs(root.left); dfs(root.right); } private HashMap<String,Long> cache=new HashMap <>();public long sum (TreeNode root) { if (root==null ) { return 0 ; } if (cache.containsKey(root.toString())) { return cache.get(root.toString()); } cache.put(root.toString(),root.val+sum(root.left)+sum(root.right)); return cache.get(root.toString()); }
解法三
标准O(N)的解法
private long mod=1000000007 ; List<Long> sum=new ArrayList <>(); public int maxProduct (TreeNode root) { long max=-1 ; long sumAll=dfs(root); for (Long s:sum) { max=Math.max(max,s*(sumAll-s)); } return (int )(max%mod); } public long dfs (TreeNode root) { if (root==null ) { return 0 ; } sum.add(root.val+dfs(root.left)+dfs(root.right)); return sum.get(sum.size()-1 ); }
在 dfs 的过程中将子树的 sum 存起来,然后直接遍历 list,求 max(s*(sumAll-s))就 ok
这里最开始被大数据也卡了一会儿,不知道啥时候取模,其实这里题目没有那么难,相乘的结果并不会溢出 Long,如果要是溢出 Long 的话可能就要用什么带模快速乘了
序列化是将一个数据结构或者对象转换为连续的比特位的操作,进而可以将转换后的数据存储在一个文件或者内存中,同时也可以通过网络传输到另一个计算机环境,采取相反方式重构得到原数据。
请设计一个算法来实现二叉树的序列化与反序列化。这里不限定你的序列 / 反序列化算法执行逻辑,你只需要保证一个二叉树可以被序列化为一个字符串并且将这个字符串反序列化为原始的树结构。
示例:
你可以将以下二叉树: 1 / \ 2 3 / \ 4 5 序列化为 "[1,2,3,null,null,4,5]"
提示: 这与 LeetCode 目前使用的方式一致,详情请参阅 LeetCode 序列化二叉树的格式。你并非必须采取这种方式,你也可以采用其他的方法解决这个问题。
说明: 不要使用类的成员 / 全局 / 静态变量来存储状态,你的序列化和反序列化算法应该是无状态的。
解法一
层序遍历非递归的方式
public String serialize (TreeNode root) { if (root==null ) { return "" ; } StringBuilder sb=new StringBuilder (); Queue<TreeNode> queue=new LinkedList <>(); queue.add(root); while (!queue.isEmpty()){ TreeNode cur=queue.poll(); if (cur!=null ) { sb.append(cur.val+"," ); queue.add(cur.left); queue.add(cur.right); }else { sb.append("null," ); } } return sb.toString(); } public TreeNode deserialize (String data) { if ("" .equals(data)) { return null ; } String[] treeData=data.split("," ); int index=0 ; TreeNode root=node(treeData[index]); Queue<TreeNode> queue=new LinkedList <>(); queue.add(root); while (!queue.isEmpty()){ TreeNode cur=queue.poll(); cur.left=node(treeData[++index]); if (cur.left!=null ) { queue.add(cur.left); } cur.right=node(treeData[++index]); if (cur.right!=null ) { queue.add(cur.right); } } return root; } public TreeNode node (String str) { if (!"null" .equals(str)) { return new TreeNode (Integer.valueOf(str)); } return null ; }
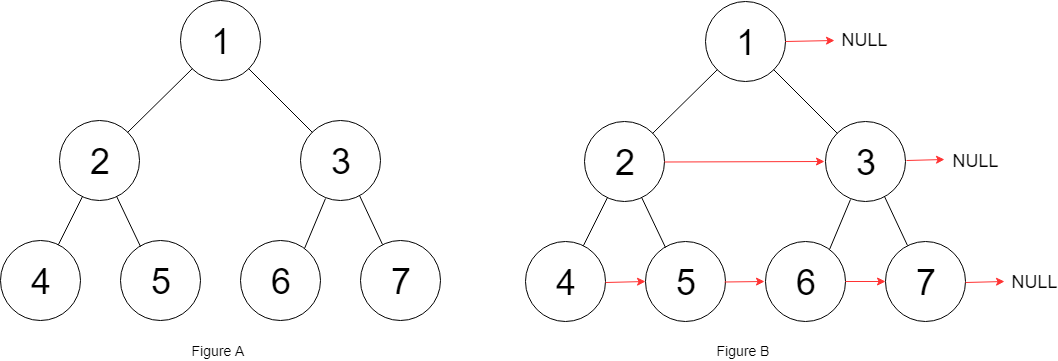
解法二
前序遍历递归方式,我们将序列化的结果存在一个queue中,然后从头开始取,因为是前序遍历,所以整体结构肯定是【root,root.left,root.right】
反序列化关键就是如何区分左右子树,仅仅依靠一个前序遍历是无法重建二叉树的,所以我们可以做一些小手段,在序列化节点为空的时候加入null字符,这样左右节点就会被连续的两个[null,null]分隔开,方便重建
eg. 示例一: 1,2,null,null,3,4,null,null,5,null,null
public TreeNode node (String str) { if (!"null" .equals(str)) { return new TreeNode (Integer.valueOf(str)); } return null ; } public String serialize (TreeNode root) { if (root==null ) { return "null" ; } return root.val+"," +serialize(root.left)+"," +serialize(root.right); } public TreeNode deserialize (String data) { if ("" .equals(data)) { return null ; } String[] dataTree=data.split("," ); Queue<String> queue=new LinkedList <>(Arrays.asList(dataTree)); return deserialize(queue); } public TreeNode deserialize (Queue<String> queue) { String val=queue.poll(); if ("null" .equals(val)) { return null ; } TreeNode root=node(val); root.left=deserialize(queue); root.right=deserialize(queue); return root; }
解法三
补充一个 go 的写法,和解法二的思路是一样的
type Codec struct {} func Constructor () return Codec{} } func (this *Codec) string { if root == nil { return "nil" } return strconv.Itoa(root.Val) + "," + this.serialize(root.Left) + "," + this.serialize(root.Right) } func (this *Codec) string ) *TreeNode { queue := strings.Split(data, "," ) return this.des(&queue) } func (this *Codec) string ) *TreeNode { if len (*queue) == 0 { return nil } cur := (*queue)[0 ] *queue = (*queue)[1 :] if cur == "nil" { return nil } val, _ := strconv.Atoi(cur) root := &TreeNode{Val: val} root.Left = this.des(queue) root.Right = this.des(queue) return root }
序列化是将数据结构或对象转换为一系列位的过程,以便它可以存储在文件或内存缓冲区中,或通过网络连接链路传输,以便稍后在同一个或另一个计算机环境中重建。
设计一个算法来序列化和反序列化二叉搜索树。 对序列化/反序列化算法的工作方式没有限制。 您只需确保二叉搜索树可以序列化为字符串,并且可以将该字符串反序列化为最初的二叉搜索树。
编码的字符串应尽可能紧凑。
注意: 不要使用类成员/全局/静态变量来存储状态。 你的序列化和反序列化算法应该是无状态的。
解法一
题目说 编码的字符串应尽可能紧凑,所以直接把上面 297 的搬过来其实不太好,因为会有很多 null 字符,并且也没有用到题目二bst的条件,bst只需要知道一个前序或者后序就可以还原整棵树,题目就变成了根据前序/后序和中序还原二叉树
golang新手,用golang写了一发,感觉写复杂了(官方解法中还有更加激进的压缩编码的方式,感觉有点偏了)
type Codec struct {} func Constructor () return Codec{} } func (this *Codec) string { if root == nil { return "" } var queue []string var dfs func (root *TreeNode) dfs = func (root *TreeNode) if root == nil { return } queue = append (queue, strconv.Itoa(root.Val)) dfs(root.Left) dfs(root.Right) } dfs(root) return strings.Join(queue, "," ) } func (this *Codec) string ) *TreeNode { if data == "" { return nil } queue := strings.Split(data, "," ) inOrder := make ([]int , len (queue)) for i, v := range queue { inOrder[i], _ = strconv.Atoi(v) } preOrder := make ([]int , len (inOrder)) copy (preOrder, inOrder) sort.Ints(inOrder) var dfs func (preOrder, inOrder []int ) dfs = func (preOrder, inOrder []int ) if len (inOrder) == 0 { return nil } root := &TreeNode{Val: preOrder[0 ]} rootIdx := 0 for i, v := range inOrder { if v == preOrder[0 ] { rootIdx = i break } } root.Left = dfs(preOrder[1 :rootIdx+1 ], inOrder[:rootIdx]) root.Right = dfs(preOrder[rootIdx+1 :], inOrder[rootIdx+1 :]) return root } return dfs(preOrder, inOrder) }
输入一个整数数组,判断该数组是不是某二叉搜索树的后序遍历结果。如果是则返回 true,否则返回 false。假设输入的数组的任意两个数字都互不相同。
参考以下这颗二叉搜索树:
示例 1:
示例 2:
提示:
数组长度 <= 1000
解法一
核心在于意识到最后一个节点是根节点
public boolean verifyPostorder (int [] postorder) { if (postorder==null || postorder.length<=0 ) return true ; return verify(postorder,0 ,postorder.length-1 ); } public boolean verify (int [] postorder,int left,int right) { if (left>=right) return true ; int root=postorder[right]; int index=left-1 ; for (int i=right-1 ;i>=left;i--){ if (postorder[i]<root){ index=i; break ; } } for (int i=index;i>=left;i--){ if (postorder[i]>root){ return false ; } } return verify(postorder,left,index) && verify(postorder,index+1 ,right-1 ); }
这题 WA 了 3 发,前两发是代码逻辑的问题,想简化代码,结果把自己带坑里面去了,最后一次是因为一个变量设置的问题,代码中已经注释
UPDATE: 2020.7.14
重写了下,这样写就不会有奇怪的 WA 点了,还是要多注意细节和边界
func verifyPostorder (post []int ) bool { return dfs(post, 0 , len (post)-1 ) } func dfs (post[] int , left int , right int ) bool { if left>=right{ return true } var p = right-1 for p >= left && post[p] > post[right]{ p-- } for i := p; i >= left; i--{ if post[i] > post[right]{ return false } } return dfs(post, left, p) && dfs(post, p+1 ,right-1 ) }
解法二
单调栈的解法,放在 单调栈专题 中
给定一个不含重复元素的整数数组。一个以此数组构建的最大二叉树定义如下:
二叉树的根是数组中的最大元素。
左子树是通过数组中最大值左边部分构造出的最大二叉树。
右子树是通过数组中最大值右边部分构造出的最大二叉树。
通过给定的数组构建最大二叉树,并且输出这个树的根节点。
示例 :
输入:[3 ,2 ,1 ,6 ,0 ,5 ] 输出:返回下面这棵树的根节点: 6 / \ 3 5 \ / 2 0 \ 1
提示:
给定的数组的大小在 [1, 1000] 之间。
解法一
public TreeNode constructMaximumBinaryTree (int [] nums) { int n=nums.length; int [][] max=new int [n][n]; for (int i=0 ;i<n;i++){ max[i][i]=i; for (int j=i+1 ;j<n;j++){ max[i][j]=nums[j]>nums[max[i][j-1 ]]?j:max[i][j-1 ]; } } return dfs(nums,0 ,n-1 ,max); } public TreeNode dfs (int [] nums,int left,int right,int [][] max) { if (left>right) return null ; int maxIdx=max[left][right]; TreeNode root=new TreeNode (nums[maxIdx]); root.left=dfs(nums,left,maxIdx-1 ,max); root.right=dfs(nums,maxIdx+1 ,right,max); return root; }
慢的主要原因是构建这个树的话大概只会查询 logN 次(树高度)最大值,而每层查询的复杂度和为 N,所以整体的复杂度其实只要 O(NlogN),除非数组完全有序,这样每次分割都及其不均匀,数的高度为 N 时间复杂度才会到 N^2,而我这个就直接是 N^2 了 hhhhh,太菜了,预处理的思想是好的,但是还是要看具体的题目,这里其实很多的区间值都用不上(除非搞线段树🤣
解法二
这题也可以用单调栈做,明天写,这题还有个 2,明天一起做了
题目描述很辣鸡,简单来说就是在最大二叉树 A的右边插入一个 val,仍然是最大二叉树
解法一
public TreeNode insertIntoMaxTree (TreeNode root, int val) { if (root==null ){ return new TreeNode (val); } if (root.val>val){ root.right=insertIntoMaxTree(root.right,val); return root; } TreeNode newRoot=new TreeNode (val); newRoot.left=root; return newRoot; }
给定一棵二叉树,返回所有重复的子树。对于同一类的重复子树,你只需要返回其中任意一棵 的根结点即可。
两棵树重复是指它们具有相同的结构以及相同的结点值。
示例 1:
下面是两个重复的子树:
和
因此,你需要以列表的形式返回上述重复子树的根结点。
解法一
做了忘了加上了,序列化子树,用哈希表判重就行了
HashMap<String,Integer> map=new HashMap <>(); List<TreeNode> res=new ArrayList <>(); public List<TreeNode> findDuplicateSubtrees (TreeNode root) { dfs(root); return res; } public String dfs (TreeNode root) { if (root==null ){ return "null" ; } String key=root.val+dfs(root.left)+dfs(root.right); int count=map.getOrDefault(key,0 ); if (count==1 ){ res.add(root); } map.put(key,count+1 ); return key; }
这题少了 case,不加分隔符也能 A,我以为会卡这个,试了下结果没卡,100 积分到手 ==> issue
给定一个二叉搜索树和一个目标结果,如果 BST 中存在两个元素且它们的和等于给定的目标结果,则返回 true。
案例 1:
输入: 5 / \ 3 6 / \ \ 2 4 7 Target = 9 输出:True
案例 2:
输入: 5 / \ 3 6 / \ \ 2 4 7 Target = 28 输出:False
解法一
开始还想着在 logN 的解法,发现好像搞不了,而且这是个 easy 题,所以肯定就是直接中序+双指针了
func findTarget (root *TreeNode, k int ) bool { var inorder []int dfs(root, &inorder) i, j := 0 , len (inorder)-1 for i < j { if inorder[i]+inorder[j] < k { i++ } else if inorder[i]+inorder[j] > k { j-- } else { return true } } return false } func dfs (root *TreeNode, inorder *[]int ) if root == nil { return } dfs(root.Left, inorder) *inorder = append (*inorder, root.Val) dfs(root.Right, inorder) }
请考虑一颗二叉树上所有的叶子,这些叶子的值按从左到右的顺序排列形成一个 叶值序列 。
举个例子,如上图所示,给定一颗叶值序列为 (6, 7, 4, 9, 8) 的树。
如果有两颗二叉树的叶值序列是相同,那么我们就认为它们是 叶相似 的。
如果给定的两个头结点分别为 root1 和 root2 的树是叶相似的,则返回 true;否则返回 false 。
提示:
给定的两颗树可能会有 1 到 200 个结点。
给定的两颗树上的值介于 0 到 200 之间。
解法一
换成StringBuilder可能会快一点
public boolean leafSimilar (TreeNode root1, TreeNode root2) { if (root1==null || root2==null ) return false ; return dfs(root1).equals(dfs(root2)); } public String dfs (TreeNode root) { if (root==null ){ return "" ; } if (root.left==null && root.right==null ){ return "#" +root.val; } return dfs(root.left)+dfs(root.right); }
当时看到这题就着会不会又有 case 遗漏,比如不加分隔符什么的,结果看到 github 已经有人先手提交了
给你一棵根为 root 的二叉树,请你返回二叉树中好节点的数目。
「好节点」X 定义为:从根到该节点 X 所经过的节点中,没有任何节点的值大于 X 的值。
示例 1:
输入:root = [3 ,1 ,4 ,3 ,null ,1 ,5 ] 输出:4 解释:图中蓝色节点为好节点。 根节点 (3 ) 永远是个好节点。 节点 4 -> (3 ,4 ) 是路径中的最大值。 节点 5 -> (3 ,4 ,5 ) 是路径中的最大值。 节点 3 -> (3 ,1 ,3 ) 是路径中的最大值。
示例 2:
输入:root = [3 ,3 ,null ,4 ,2 ] 输出:3 解释:节点 2 -> (3 , 3 , 2 ) 不是好节点,因为 "3" 比它大。
示例 3:
输入:root = [1 ] 输出:1 解释:根节点是好节点。
提示:
二叉树中节点数目范围是 [1, 10^5] 。
每个节点权值的范围是 [-10^4, 10^4] 。
解法一
26th 双周赛的 t3,水题
int count=0 ;public int goodNodes (TreeNode root) { if (root==null ) return 0 ; dfs(root,root.val); return count; } public void dfs (TreeNode root,int max) { if (root==null ){ return ; } if (max<=root.val){ count++; max=root.val; } dfs(root.left,max); dfs(root.right,max); }
给定一个二叉搜索树,同时给定最小边界L 和最大边界 R。通过修剪二叉搜索树,使得所有节点的值在[L, R]中 (R>=L) 。你可能需要改变树的根节点,所以结果应当返回修剪好的二叉搜索树的新的根节点。
示例 1:
输入: 1 / \ 0 2 L = 1 R = 2 输出: 1 \ 2
示例 2:
输入: 3 / \ 0 4 \ 2 / 1 L = 1 R = 3 输出: 3 / 2 / 1
解法一
没啥好说的,递归后序遍历就完事了,树的题还是挺套路的
public TreeNode trimBST (TreeNode root, int L, int R) { if (root==null ){ return root; } root.left=trimBST(root.left,L,R); root.right=trimBST(root.right,L,R); if (root.val<L){ return root.right; } if (root.val>R){ return root.left; } return root; }
Difficulty: 中等
给定二叉树根结点 root ,此外树的每个结点的值要么是 0,要么是 1。
返回移除了所有不包含 1 的子树的原二叉树。
( 节点 X 的子树为 X 本身,以及所有 X 的后代。)
示例 1 : 输入:[1 ,null,0 ,0 ,1 ] 输出:[1 ,null,0 ,null,1 ] 解释: 只有红色节点满足条件“所有不包含 1 的子树”。 右图为返回的答案。
示例 2 : 输入:[1 ,0 ,1 ,0 ,0 ,0 ,1 ] 输出:[1 ,null,1 ,null,1 ]
示例 3 : 输入:[1 ,1 ,0 ,1 ,1 ,0 ,1 ,0 ] 输出:[1 ,1 ,0 ,1 ,1 ,null,1 ]
说明:
给定的二叉树最多有 100 个节点。
每个节点的值只会为 0 或 1 。
解法一
和上面差不多,感觉应该是是 easy。
func pruneTree (root *TreeNode) if root == nil { return nil } root.Left = pruneTree(root.Left) root.Right = pruneTree(root.Right) if root.Left == nil && root.Right==nil && root.Val == 0 { return nil } return root }
题目就不 copy 了,二叉树只有一个值,水题
解法一
public boolean isUnivalTree (TreeNode root) { return dfs(root,root.val); } public boolean dfs (TreeNode root,int val) { if (root==null ) return true ; return root.val==val && dfs(root.left,val) && dfs(root.right,val); }
有两位极客玩家参与了一场「二叉树着色」的游戏。游戏中,给出二叉树的根节点 root,树上总共有 n 个节点,且 n 为奇数,其中每个节点上的值从 1 到 n 各不相同。
游戏从「一号」玩家开始(「一号」玩家为红色,「二号」玩家为蓝色),最开始时,
「一号」玩家从 [1, n] 中取一个值 x(1 <= x <= n);
「二号」玩家也从 [1, n] 中取一个值 y(1 <= y <= n)且 y != x。
「一号」玩家给值为 x 的节点染上红色,而「二号」玩家给值为 y 的节点染上蓝色。
之后两位玩家轮流进行操作,每一回合,玩家选择一个他之前涂好颜色的节点,将所选节点一个 未着色 的邻节点(即左右子节点、或父节点)进行染色。
如果当前玩家无法找到这样的节点来染色时,他的回合就会被跳过。
若两个玩家都没有可以染色的节点时,游戏结束。着色节点最多的那位玩家获得胜利 ✌️。
现在,假设你是「二号」玩家,根据所给出的输入,假如存在一个 y 值可以确保你赢得这场游戏,则返回 true;若无法获胜,就请返回 false。
示例:
输入:root = [1 ,2 ,3 ,4 ,5 ,6 ,7 ,8 ,9 ,10 ,11 ], n = 11 , x = 3 输出:True 解释:第二个玩家可以选择值为 2 的节点。
提示:
二叉树的根节点为 root,树上由 n 个节点,节点上的值从 1 到 n 各不相同。
n 为奇数。1 <= x <= n <= 100
解法一
第一个选手选择了一个节点之后,将二叉树实际上划分为了 3 个区域,左孩子区域,右孩子区域,还有父节点所在区域,三个区域以 x 为界限,没有交集,第二个选手需要在三个区域中选取一个区域,使自己能赢,很明显我们肯定要选最大的那个区域,所以我们只需要判断最大的区域是否比剩下其他部分和都要大就行了
int max=0 ;public boolean btreeGameWinningMove (TreeNode root, int n, int x) { dfs(root,x,n); return max>n-max; } public int dfs (TreeNode root,int x,int n) { if (root==null ) return 0 ; int left=dfs(root.left,x,n); int right=dfs(root.right,x,n); if (root.val==x){ max=Math.max(left,max); max=Math.max(right,max); max=Math.max(n-left-right-1 ,max); } return left+right+1 ; }
在二叉树中,根节点位于深度 0 处,每个深度为 k 的节点的子节点位于深度 k+1 处。
如果二叉树的两个节点深度相同,但父节点不同 ,则它们是一对堂兄弟节点 。
我们给出了具有唯一值的二叉树的根节点 root,以及树中两个不同节点的值 x 和 y。
只有与值 x 和 y 对应的节点是堂兄弟节点时,才返回 true。否则,返回 false。
示例 1:
输入:root = [1 ,2 ,3 ,4 ], x = 4 , y = 3 输出:false
示例 2:
输入:root = [1 ,2 ,3 ,null ,4 ,null ,5 ], x = 5 , y = 4 输出:true
示例 3:
输入:root = [1 ,2 ,3 ,null ,4 ], x = 2 , y = 3 输出:false
提示:
二叉树的节点数介于 2 到 100 之间。
每个节点的值都是唯一的、范围为 1 到 100 的整数。
解法一
二叉树水题(3 天没刷新题了,再不刷几道实在是说不过其了,刷题还是要保持手感啊)
func isCousins (root *TreeNode, x int , y int ) bool { var depX = -1 var pX *TreeNode var depY = -1 var pY *TreeNode var dfs func (root, parent *TreeNode, x, y int , depth int ) dfs = func (root, parent *TreeNode, x, y int , depth int ) if root == nil { return } if root.Val == x { depX = depth pX = parent return } if root.Val == y { depY = depth pY = parent return } dfs(root.Left, root, x, y, depth+1 ) dfs(root.Right, root, x, y, depth+1 ) } dfs(root, nil , x, y, 0 ) return pX != pY && depX == depY }
有一个小的优化点还是挺有意思的,就是 return 的地方,一开始没考虑这么多,AC 了之后感觉不对,是不是 LC 又少 CASE 了,结果仔细一想发现这里是个优化点😁
给定整数 n 和 k,找到 1 到 n 中字典序第 k 小的数字。
注意:1 ≤ k ≤ n ≤ 1e9。
示例 :
输入: n: 13 k: 2 输出: 10 解释: 字典序的排列是 [1 , 10 , 11 , 12 , 13 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 ],所以第二小的数字是 10 。
解法一
一开始看了评论区说了 10 叉树,然后我就顺着这个思路去想了,然后就直接去前序遍历了,然后就 T 了,这里看下数据范围就知道肯定是过不了的
public int findKthNumber (int n, int k) { for (int i=1 ;i<=9 ;i++) { dfs(i,n,k); } return res; } int idx=0 ,res=-1 ;public void dfs (int cur,int n,int k) { if (res!=-1 ) return ; if (cur>n) return ; idx++; if (k==idx){ res=cur; return ; } for (int i=0 ;i<=9 ;i++) { dfs(cur*10 +i,n,k); } }
解法二
直接遍历肯定是行不通,那么就只能想办法跳过一些节点,这里我们就可以通过计算每个节点的子节点的个数来判断第 k 个是不是在该节点下,而子节点的个数就可以用Min(n+1,next*10)-cur计算得到,next是和 cur 相邻的节点,n是最大值,画个图就懂了
func findKthNumber (n int , k int ) int { var cur = 1 for k > 1 { count := getChild(cur, n) if count < k { cur++ k-=count } else { cur *= 10 k-- } } return cur } func getChild (cur int , n int ) int { var count = 0 var next = cur+1 for cur <= n { count += Min(n+1 , next) - cur cur *= 10 next *= 10 } return count } func Min (a, b int ) int { if a < b { return a } return b }
给定一个整数 n, 返回从 1 到 n 的字典顺序。
例如,
给定 n =1 3,返回 [1,10,11,12,13,2,3,4,5,6,7,8,9] 。
请尽可能的优化算法的时间复杂度和空间复杂度。 输入的数据 n 小于等于 5,000,000。
解法一
先做的上面那一题,再做这一题就简单多了,前面 tle 的方法就是这里的正解,十叉树的前序遍历
List<Integer> res=new ArrayList <>(); public List<Integer> lexicalOrder (int n) { for (int i=1 ;i<=9 ;i++){ dfs(i,n); } return res; } public void dfs (int cur,int n) { if (cur>n) return ; res.add(cur); for (int i=0 ;i<=9 ;i++){ dfs(cur*10 +i,n); } }
我们从二叉树的根节点 root 开始进行深度优先搜索。
在遍历中的每个节点处,我们输出 D 条短划线(其中 D 是该节点的深度),然后输出该节点的值。(如果节点的深度为 D,则其直接子节点的深度为 D + 1。根节点的深度为 0)。
如果节点只有一个子节点,那么保证该子节点为左子节点。
给出遍历输出 S,还原树并返回其根节点 root。
示例 1:
输入:"1-2--3--4-5--6--7" 输出:[1 ,2 ,5 ,3 ,4 ,6 ,7 ]
示例 2:
输入:"1-2--3---4-5--6---7" 输出:[1 ,2 ,5 ,3 ,null ,6 ,null ,4 ,null ,7 ]
示例 3:
输入:"1-401--349---90--88" 输出:[1 ,401 ,null ,349 ,88 ,90 ]
提示:
解法一
抄答案,第一天看了几分钟,一开始想写递归,直接看了答案,第二天还是没有完整的写出来,其实这题迭代会好理解很多,递归的看了下,有点不好理解,很 trick
public TreeNode recoverFromPreorder (String S) { Deque<TreeNode> stack=new ArrayDeque (); int i=0 ; while (i<S.length()){ int depth=0 ; while (i<S.length() && S.charAt(i)=='-' ) { depth++; i++; } int val=0 ; while (i<S.length() && S.charAt(i)>='0' && S.charAt(i)<='9' ){ val=val*10 +S.charAt(i)-48 ; i++; } TreeNode node=new TreeNode (val); if (depth==stack.size()){ if (!stack.isEmpty()) stack.peek().left=node; }else { while (depth!=stack.size()){ stack.pop(); } stack.peek().right=node; } stack.push(node); } while (stack.size()!=1 ) stack.pop(); return stack.pop(); }
给你一个树,请你 按中序遍历 重新排列树,使树中最左边的结点现在是树的根,并且每个结点没有左子结点,只有一个右子结点。
示例 :
输入:[5 ,3 ,6 ,2 ,4 ,null ,8 ,1 ,null ,null ,null ,7 ,9 ] 5 / \ 3 6 / \ \ 2 4 8 / / \ 1 7 9 输出:[1 ,null ,2 ,null ,3 ,null ,4 ,null ,5 ,null ,6 ,null ,7 ,null ,8 ,null ,9 ] 1 \ 2 \ 3 \ 4 \ 5 \ 6 \ 7 \ 8 \ 9
提示:
给定树中的结点数介于 1 和 100 之间。每个结点都有一个从 0 到 1000 范围内的唯一整数值。
解法一
go 中序遍历配合全局变量,没啥好说的(看评论区很多人直接 new TreeNode 感觉不太好吧,题目的意思不是在原树上改么?)
func increasingBST (root *TreeNode) var dfs func (root *TreeNode) dummyNode:=&TreeNode{} last:=dummyNode dfs = func (root *TreeNode) if root==nil { return } dfs(root.Left) root.Left=nil last.Right=root last = root dfs(root.Right) } dfs(root) return dummyNode.Right }
这题和 面试题 17.12. BiNode 解法是一摸一样的,但是这个 sb 题的描述我是真没看懂,结合评论区和 case 才知道到底要干啥,看评论区好像都整的挺明白的,一度以为我理解能力出了问题
Difficulty: 中等
给定一个有 N 个结点的二叉树的根结点 root,树中的每个结点上都对应有 node.val 枚硬币,并且总共有 N 枚硬币。
在一次移动中,我们可以选择两个相邻的结点,然后将一枚硬币从其中一个结点移动到另一个结点。(移动可以是从父结点到子结点,或者从子结点移动到父结点。)。
返回使每个结点上只有一枚硬币所需的移动次数。
示例 1:
输入:[3 ,0 ,0 ] 输出:2 解释:从树的根结点开始,我们将一枚硬币移到它的左子结点上,一枚硬币移到它的右子结点上。
示例 2:
输入:[0 ,3 ,0 ] 输出:3 解释:从根结点的左子结点开始,我们将两枚硬币移到根结点上 [移动两次]。然后,我们把一枚硬币从根结点移到右子结点上。
示例 3:
示例 4:
提示:
1<= N <= 100
0 <= node.val <= N
解法一
一开始直接想出来的做法,后面看了其他人的解法发现还不太一样😂,不过我还是感觉我的方法更好理解
func distributeCoins (root *TreeNode) int { var res = 0 var Abs = func (a int ) int { if a < 0 { return -a } return a } var dfs func (*TreeNode) int , int ) dfs = func (root *TreeNode) int , int ) { if root == nil { return 0 , 0 } lCount, lCoins := dfs(root.Left) res += Abs(lCount - lCoins) rCount, rCoins := dfs(root.Right) res += Abs(rCount - rCoins) return 1 + lCount + rCount, root.Val + lCoins + rCoins } dfs(root) return res }
解法二
其他人的做法,dfs 返回节点的盈亏值(节点数和金币数的差值),盈亏值绝对值之和就是总体的转移次数(所以两种解法其实是一样的,只是计算的时间不一样,我的是函数返回后计算盈亏,而下面的解法是返回前计算盈亏,感觉我的更好理解😂)
func distributeCoins (root *TreeNode) int { var res = 0 var Abs = func (a int ) int { if a < 0 { return -a } return a } var dfs func (*TreeNode) int dfs = func (root *TreeNode) int { if root == nil { return 0 } left := dfs(root.Left) right := dfs(root.Right) res += Abs(left) + Abs(right) return root.Val + left + right - 1 } dfs(root) return res }
Difficulty: 困难
二叉搜索树中的两个节点被错误地交换。
请在不改变其结构的情况下,恢复这棵树。
示例 1:
输入:[1 ,3 ,null,null,2 ] 1 / 3 \ 2 输出:[3 ,1 ,null,null,2 ] 3 / 1 \ 2
示例 2:
输入:[3 ,1 ,4 ,null,null,2 ] 3 / \ 1 4 / 2 输出:[2 ,1 ,4 ,null,null,3 ] 2 / \ 1 4 / 3
进阶:
使用 O(n ) 空间复杂度的解法很容易实现。
你能想出一个只使用常数空间的解决方案吗?
解法一
中序遍历,记录下位置不对的节点,最后交换他们的值就行了
func recoverTree (root *TreeNode) var node1 *TreeNode var node2 *TreeNode var pre *TreeNode var dfs func (*TreeNode) dfs = func (root *TreeNode) if root == nil { return } dfs(root.Left) if pre != nil && root.Val < pre.Val { if node1 == nil { node1 = pre } node2 = root } pre = root dfs(root.Right) } dfs(root) node1.Val, node2.Val = node2.Val, node1.Val }
这种解法严格来说空间复杂度并不是 O(1),递归会有系统栈的开销,空间复杂度应该是 O(h),h 是树的高度,真正的 O(1) 的做法应该是 Morris 遍历,这种解法就称得上 hard 了
Difficulty: 中等
给你一棵二叉树,请你返回层数最深的叶子节点的和。
示例:
输入:root = [1,2,3,4,5,null,6,7,null,null,null,null,8] 输出:15
提示:
树中节点数目在 1 到 10^4 之间。
每个节点的值在 1 到 100 之间。
解法一
BFS 没啥好说的,DFS 的挺有意思
func deepestLeavesSum (root *TreeNode) int { var dfs func (*TreeNode, int ) var maxDep = 0 var sum = 0 dfs = func (root *TreeNode, dep int ) if root == nil { return } if maxDep == dep { sum += root.Val } if dep > maxDep { sum = root.Val maxDep = dep } dfs(root.Left, dep+1 ) dfs(root.Right, dep+1 ) } dfs(root, 0 ) return sum }
树形 DP(大概)
2020.5.10 更新,在看了左神的书后,大概了解了树形 DP,所谓的树形 DP 实际上就是把递推方程搬到了树结构上,按我的理解树形 DP 很大的特点就是最终的解可能存在于树上每个节点,像我下面的题有的暴力解用的就是双重递归,就是 dfs 遍历没个节点,然后再对每个节点递归求解,但是对根节点求解的时候,实际上其他的子节点都成了子问题,所以后面再对子节点求解的时候问题就重复了,所以就可以采用后序遍历,自底向上,先求左右节点的值再更新根节点,下面的题其实我不知道到底是不是属于树形 DP,可能太简单了,但是再我看来解法比较统一,很有套路所以整理到一起 ,我查了下网上介绍的树形 DP 还是挺难的,后面有时间了解后再来记录
给定一个二叉树,判断它是否是高度平衡的二叉树。
本题中,一棵高度平衡二叉树定义为:
一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1
示例 1:
给定二叉树 [3,9,20,null,null,15,7]
返回 true 。
示例 2:
给定二叉树 [1,2,2,3,3,null,null,4,4]
返回 false 。
解法一
暴力法,结合上面的 [二叉树最大深度](#104. 二叉树的最大深度),自顶向下 ,求左右子树的高度差
public boolean isBalanced (TreeNode root) { if (root==null ) return true ; if (Math.abs(hight(root.left)-hight(root.right))>1 ) { return false ; } return isBalanced(root.left) && isBalanced(root.right); } public int hight (TreeNode root) { if (root==null ) { return 0 ; } return Math.max(hight(root.right),hight(root.left))+1 ; }
自顶向下,先判断根节点,然后判断左右子树,很明显。在判断左右子树的时候,会重复的遍历判断根节点的时候已经遍历过的节点,时间复杂度应该是O(N^2)
解法二
自底向上,利用一个实例变量保存结果,其实就是在上面的求 heigh 过程中将左右子树的高度先取出来直接比较,如果差距大于 1 就直接记录下结果 false,但是其实这里还是可以优化下
private boolean ans=true ;public boolean isBalanced (TreeNode root) { if (root==null ) return true ; hight(root); return ans; } public int hight (TreeNode root) { if (root==null ) { return 0 ; } int left=hight(root.left); int right=hight(root.right); if (Math.abs(left-right)>1 ) { ans=false ; } return Math.max(left,right)+1 ; }
自底向上,只需要遍历一遍二叉树就可以得到结果,时间复杂度O(N)
解法三
public boolean isBalanced (TreeNode root) { if (root==null ) return true ; return hight(root)!=-1 ; } public int hight (TreeNode root) { if (root==null ) { return 0 ; } int left=hight(root.left); if (left==-1 ) { return -1 ; } int right=hight(root.right); if (right==-1 ) { return -1 ; } return Math.abs(left-right)>1 ?-1 :Math.max(left,right)+1 ; }
在不符合的时候一路return -1 节省后面的计算
给定一个二叉树,计算整个树的坡度。
一个树的节点的坡度定义即为,该节点左子树的结点之和和右子树结点之和的差的绝对值。空结点的的坡度是 0。
整个树的坡度就是其所有节点的坡度之和。
示例:
输入: 1 / \ 2 3 输出:1 解释: 结点的坡度 2 : 0 结点的坡度 3 : 0 结点的坡度 1 : |2 -3 | = 1 树的坡度 : 0 + 0 + 1 = 1
注意:
任何子树的结点的和不会超过 32 位整数的范围。
坡度的值不会超过 32 位整数的范围。.
解法一
很快写出来的解法,发现这题和上面的 平衡二叉树 有异曲同工之妙!
public int findTilt (TreeNode root) { if (root==null ) { return 0 ; } return findTilt(root.left)+findTilt(root.right)+Math.abs(childSum(root.left)-childSum(root.right)); } public int childSum (TreeNode root) { if (root==null ) { return 0 ; } return childSum(root.left)+childSum(root.right)+root.val; }
嵌套递归,相当暴力
解法二
上面的做法确实有点可惜,其实在计算 childSum 的时候就可以字节把坡度算出来然后累加就是整体的坡度
int tilt=0 ;public int findTilt (TreeNode root) { childSum(root); return tilt; } public int childSum (TreeNode root) { if (root==null ) { return 0 ; } int left=childSum(root.left); int right=childSum(root.right); tilt+=Math.abs(left-right); return left+right+root.val; }
给定一棵二叉树,你需要计算它的直径长度。一棵二叉树的直径长度是任意两个结点路径长度中的最大值。这条路径可能穿过根结点。
示例 :
返回 3, 它的长度是路径 [4,2,1,3] 或者 [5,2,1,3]。
注意: 两结点之间的路径长度是以它们之间边的数目表示
解法一
树的题目做多了,发现其实也就几种题型,都很熟悉,这题就和上面的 二叉树的坡度 ,平衡二叉树 很类似,这题需要注意直径不一定过根节点
int max=Integer.MIN_VALUE;public int diameterOfBinaryTree (TreeNode root) { if (root==null ) { return 0 ; } hight(root); return max; } public int hight (TreeNode node) { if (node==null ) { return 0 ; } int left=hight(node.left); int right=hight(node.right); max=Math.max(left+right,max); return Math.max(left,right)+1 ; }
解法二
和之前一样,先写了个暴力的嵌套递归😂,代码确实简介,难道这就是暴力美学么,i 了
public int diameterOfBinaryTree (TreeNode root) { return root==null ?0 :Math.max(hight(root.left)+hight(root.right),Math.max(diameterOfBinaryTree(root.right),diameterOfBinaryTree(root.left))); } public int hight (TreeNode node) { return node==null ?0 :Math.max(hight(node.left),hight(node.right))+1 ; }
给定一个非空 二叉树,返回其最大路径和。
本题中,路径被定义为一条从树中任意节点出发,达到任意节点的序列。该路径至少包含一个节点,且不一定经过根节点。
示例 1:
示例 2:
输入:[-10 ,9 ,20 ,null ,null ,15 ,7 ] -10 / \ 9 20 / \ 15 7 输出:42
错误解法
先上一个错误答案,过了 71/93 个 case(lc 的 case 好少)
public int maxPathSum (TreeNode root) { if (root==null ) { return Integer.MIN_VALUE; } if (root.left==null && root.right==null ) { return root.val; } int res=helper(root); return Math.max(res,Math.max(maxPathSum(root.left),maxPathSum(root.right))); } public int helper (TreeNode root) { if (root==null ) return Integer.MIN_VALUE;; if (root.left==null && root.right==null ) { return root.val; } int left=helper(root.left); int right=helper(root.right); return root.val+(left>0 ?left:0 )+(right>0 ?right:0 ); }
我一开始的想法是按照根节点来讨论的,每个节点的最大值就是 左右子树的最大路径和(大于 0)加上当前节点的值,改了半天 WA 了几发后发现是有问题的
比如这样的,2 为根的最长路径是 1,2,9 但是这个在 1 为根的节点中是不合法的,所以我们需要的只有单边的路径和,如上图的树,我们需要的就是 2->9 这条路径,所以我们需要再添加一个求最长路径的函数
解法二
可 AC,但是效率较低
public int maxPathSum (TreeNode root) { if (root==null ) { return Integer.MIN_VALUE; } if (root.left==null && root.right==null ) { return root.val; } int res=helper(root); return Math.max(res,Math.max(maxPathSum(root.left),maxPathSum(root.right))); } public int helper (TreeNode root) { if (root==null ) return Integer.MIN_VALUE; if (root.left==null && root.right==null ) { return root.val; } int left=dfs(root.left); int right=dfs(root.right); return root.val+(left>0 ?left:0 )+(right>0 ?right:0 ); } private HashMap<String,Integer> cache=new HashMap <>();public int dfs (TreeNode root) { if (root==null ) { return Integer.MIN_VALUE; } if (cache.containsKey(root.toString())) { return cache.get(root.toString()); } int left=dfs(root.left); int right=dfs(root.right); int max=Math.max(left,right); cache.put(root.toString(),root.val+(max>0 ?max:0 )); return root.val+(max>0 ?max:0 ); }
解法三
这个解法其实就是将我前面的代码逻辑简化了,核心的思路还是一样的
private int res=Integer.MIN_VALUE;public int maxPathSum (TreeNode root) { helper(root); return res; } public int helper (TreeNode root) { if (root==null ) return 0 ; int left=Math.max(helper(root.left),0 ); int right=Math.max(helper(root.right),0 ); res=Math.max(res,root.val+left+right); return root.val+Math.max(left,right); }
在递归函数中用全局变量记录最大值,最后返回的却是单边 的最大值,也就是我上面写的 dfs 函数返回的值,可以说是相当巧妙了,除此外对递归的出口也进行了简化
Update: 2020.6.21
用 go 重写一下,最近很喜欢写这种闭包的结构,感觉比较简洁
func maxPathSum (root *TreeNode) int { res:=-1 <<31 var Max =func (a,b int ) int { if a>b{ return a } return b } var dfs func (root *TreeNode) int dfs = func (root *TreeNode) int { if root==nil { return -1 <<31 } left:=Max(0 ,dfs(root.Left)) right:=Max(0 ,dfs(root.Right)) res=Max(res,left+right+root.Val) return root.Val+Max(left,right) } dfs(root) return res }
给定一个二叉树,找到最长的路径,这个路径中的每个节点具有相同值。 这条路径可以经过也可以不经过根节点。
注意 :两个节点之间的路径长度由它们之间的边数表示。
示例 1:
输入:
输出:
示例 2:
输入:
输出:
注意: 给定的二叉树不超过 10000 个结点。 树的高度不超过 1000。
错误解法
其实写了一会儿就意识到和上面的 [124. 二叉树的最大路径和](#124-二叉树的最大路径和),543. 二叉树的直径 是一样的思路,但是自己还是没写好,递归函数的写着写着就写变了,脱离了最开始的定义
public int longestUnivaluePath (TreeNode root) { dfs(root); return res; } int res=0 ;public int dfs (TreeNode root) { if (root==null ){ return 0 ; } int leftMax=dfs(root.left); int rightMax=dfs(root.right); int flag=0 ; if (root.left!=null && root.left.val==root.val){ flag++; leftMax++; } if (root.right!=null && root.right.val==root.val){ flag++; rightMax++; } if (flag==2 ){ res=Math.max(res,leftMax+rightMax); } res=Math.max(res,Math.max(leftMax,rightMax)); return flag==0 ?0 :Math.max(leftMax,rightMax); }
解法一
在看了题解后对上面错误解法的纠正
public int longestUnivaluePath (TreeNode root) { if (root==null ) return 0 ; dfs(root); return res; } int res=0 ;public int dfs (TreeNode root) { if (root==null ){ return 0 ; } int leftMax=dfs(root.left); int rightMax=dfs(root.right); if (root.left!=null ){ leftMax=root.left.val==root.val?leftMax+1 :0 ; } if (root.right!=null ){ rightMax=root.right.val==root.val?rightMax+1 :0 ; } res=Math.max(res,leftMax+rightMax); return Math.max(leftMax,rightMax); }
注意 dfs 函数的定义:以 root 开头的最长同值路径
既然是以 root 开头,所以代表的其实是单侧 的最长路径,也就是说这个路径不能穿过 root,所以我们要分别求左右的值,然后取最大值,再判断和左右节点是否相等
再然后我们需要判断 root 和左右节点值是否相等,如果和左右节点不想等,那么leftMax和rightMax应该直接置为 0,不应该再代入做计算,上面的错误解法就是错在这里,如果相等那就应该+1,然后统计最大值的时候也就可以很轻松的包含所有的 3 种情况
这里为什么要先求最大值,再判断,先判断在求最大值不行么?
其实想想就知道不行,先判断其实相当于前序遍历,在访问节点第一次的时候如果不符合条件就直接返回了,这样根本无法遍历完所有的节点自然是不行,所以这种类型的一般都是后序遍历,待子节点都处理完之后再返回根节点做处理,和分治的思想很像
Update: 2020.6.21
go 重写一遍,换了个方式,统计节点个数最后减一
func longestUnivaluePath (root *TreeNode) int { if root==nil { return 0 } var Max=func (a,b int ) int { if a>b{return a} return b } var res=0 var dfs func (root *TreeNode) int dfs = func (root *TreeNode) int { if root==nil { return 0 } left := 1 +dfs(root.Left) right := 1 +dfs(root.Right) if root.Left==nil || root.Val!=root.Left.Val{ left=1 } if root.Right==nil || root.Val!=root.Right.Val{ right=1 } res=Max(res,left+right-1 ) return Max(left,right) } dfs(root) return res-1 }
解法二
另一种 dfs 的思路,代码更加简洁一点,但是稍微有一点不好想
public int longestUnivaluePath (TreeNode root) { if (root==null ) return 0 ; dfs(root,-1 ); return res; } int res=0 ;public int dfs (TreeNode root,int parent) { if (root==null ){ return 0 ; } int leftMax=dfs(root.left,root.val); int rightMax=dfs(root.right,root.val); res=Math.max(res,leftMax+rightMax); if (root.val==parent){ return Math.max(leftMax,rightMax)+1 ; } return 0 ; }
注意 dfs 函数的定义:以 node 父节点和 node 开始的同值路径长度
在函数中添加一个父节点的值,然后在遍历到一个节点的时候判断当前节点和父节点的关系就行了,如果和父节点不相等,那么直接返回 0,相等就返回左右最大值+1(这个+1 加的是当前节点),然后同样采用后序遍历,这个思路没有那么自然,不过也挺不错的
还有一种暴力解法,这里就不贴了
描述
给一棵二叉树,找到最长连续路径的长度。不能逆序)。
样例 1:
输入: {1 ,#,3 ,2 ,4 ,#,#,#,5 } 输出:3 说明: 这棵树如图所示 1 \ 3 / \ 2 4 \ 5 最长连续序列是 3 -4 -5 ,所以返回 3.
样例 2:
输入: {2 ,#,3 ,2 ,#,1 ,#} 输出:2 说明: 这棵树如图所示: 2 \ 3 / 2 / 1 最长连续序列是 2 -3 ,而不是 3 -2 -1 ,所以返回 2.
解法一
和上一题最长同值路径几乎一摸一样,这题 leetCode 也有,但是是会员题 ,前几天每日一题出了这个(后来改了),然后我在 lintcode 找到了,应该是同一题,随手做一下
public int longestConsecutive (TreeNode root) { dfs(root); return max; } int max=0 ;public int dfs (TreeNode root) { if (root == null ){ return 0 ; } int leftMax = Math.max(1 ,dfs(root.left)); int rightMax = Math.max(1 ,dfs(root.right)); if (root.left!=null ){ leftMax = root.val==root.left.val-1 ? leftMax+1 :1 ; } if (root.right!=null ){ rightMax = root.val==root.right.val-1 ? rightMax+1 :1 ; } max=Math.max(max,Math.max(leftMax,rightMax)); return Math.max(leftMax,rightMax); }
其实一开始写了一个很复杂的,dfs 的定义又和父节点耦合了,感觉和父节点耦合之后就很难搞,很容易搞晕,所以尽量不和父节点耦合,直接以当前节点定义
Update: 2020.6.21
func longestConsecutive (root *TreeNode) int { var Max = func (a,b int ) int { if a>b{return a} return b } var dfs func (root *TreeNode) int var res=0 dfs = func (root *TreeNode) int { if root ==nil { return 0 } left:= 1 +dfs(root.Left) right:= 1 +dfs(root.Right) if root.Left==nil ||root.Left.Val!=root.Val+1 { left=1 } if root.Right==nil ||root.Right.Val!=root.Val+1 { right=1 } res=Max(res,Max(left,right)) return Max(left,right) } dfs(root) return res }
在上次打劫完一条街道之后和一圈房屋后,小偷又发现了一个新的可行窃的地区。这个地区只有一个入口,我们称之为“根”。 除了“根”之外,每栋房子有且只有一个“父“房子与之相连。一番侦察之后,聪明的小偷意识到“这个地方的所有房屋的排列类似于一棵二叉树”。 如果两个直接相连的房子在同一天晚上被打劫,房屋将自动报警。
计算在不触动警报的情况下,小偷一晚能够盗取的最高金额。
示例 1:
输入:[3 ,2 ,3 ,null ,3 ,null ,1 ] 3 / \ 2 3 \ \ 3 1 输出:7 解释:小偷一晚能够盗取的最高金额 = 3 + 3 + 1 = 7.
示例 2:
输入:[3 ,4 ,5 ,1 ,3 ,null ,1 ] 3 / \ 4 5 / \ \ 1 3 1 输出:9 解释:小偷一晚能够盗取的最高金额 = 4 + 5 = 9.
解法一
暴力递归,应该还是写得出来
public int rob (TreeNode root) { return tryRob(root); } public int tryRob (TreeNode root) { if (root==null ) { return 0 ; } if (root.left==null && root.right==null ) { return root.val; } int res=root.val; if (root.left!=null ) { res+=tryRob(root.left.left)+tryRob(root.left.right); } if (root.right!=null ) { res+=tryRob(root.right.left)+tryRob(root.right.right); } int res2=0 ; res2=tryRob(root.left)+tryRob(root.right); return Math.max(res,res2); }
解法二
看评论区说是啥树形 dp ? 知识盲区了 hahaha
public int rob (TreeNode root) { int [] res=tryRob(root); return Math.max(res[0 ],res[1 ]); } public int [] tryRob(TreeNode root) { int [] dp=new int [2 ]; if (root==null ) { return dp; } int [] left=tryRob(root.left); int [] right=tryRob(root.right); dp[0 ]=Math.max(left[0 ],left[1 ])+Math.max(right[0 ],right[1 ]); dp[1 ]=left[0 ]+right[0 ]+root.val; return dp; }
不是我吹,就这样的题目,再遇见多少次我都写不出来这样的解(笑
2020.5.10 更新,在看了左神的书后,了解到这种其实就是树形 DP,所谓的树形 DP 实际上就是把递推方程搬到了树结构上,按我的理解树形 DP 很大的特点就是最终的解可能存在于树上每个节点,所以每个节点都是个子问题,可以从子问题推出父问题
给你一棵以 root 为根的二叉树,二叉树中的交错路径定义如下:
选择二叉树中 任意 节点和一个方向(左或者右)。
如果前进方向为右,那么移动到当前节点的的右子节点,否则移动到它的左子节点。
改变前进方向:左变右或者右变左。
重复第二步和第三步,直到你在树中无法继续移动。
交错路径的长度定义为:访问过的节点数目 - 1 (单个节点的路径长度为 0 )。
请你返回给定树中最长 交错路径 的长度。
示例 1:
输入:root = [1 ,null ,1 ,1 ,1 ,null ,null ,1 ,1 ,null ,1 ,null ,null ,null ,1 ,null ,1 ] 输出:3 解释:蓝色节点为树中最长交错路径(右 -> 左 -> 右)。
示例 2:
输入:root = [1 ,1 ,1 ,null ,1 ,null ,null ,1 ,1 ,null ,1 ] 输出:4 解释:蓝色节点为树中最长交错路径(左 -> 右 -> 左 -> 右)。
示例 3:
提示:
每棵树最多有 50000 个节点。
每个节点的值在 [1, 100] 之间。
解法一
某次周赛的 T3,树形 DP
int max=0 ;public int longestZigZag (TreeNode root) { dfs(root); return max-1 ; } public int [] dfs(TreeNode root){ int [] res=new int [2 ]; if (root==null ){ return res; } res[0 ]=dfs(root.left)[1 ]+1 ; res[1 ]=dfs(root.right)[0 ]+1 ; max=Math.max(max,Math.max(res[0 ],res[1 ])); return res; }
Update: 2020.6.21
用 go 重写(回顾)下
func longestZigZag (root *TreeNode) int { var Max = func (a,b int ) int { if a>b{return a} return b } var dfs func (root *TreeNode) int var res = 0 dfs = func (root *TreeNode) int { if root==nil { return []int {0 ,0 } } left := dfs(root.Left) right := dfs(root.Right) res=Max(res,Max(left[1 ]+1 ,right[0 ]+1 )) return []int {left[1 ]+1 ,right[0 ]+1 } } dfs(root) return res-1 }
解法二
直接搜索的做法,其实这种做法没有上面树形 dp 好理解,dfs 函数的定义会和父节点混合
int res=0 ;public int longestZigZag (TreeNode root) { dfs(root,false ); return res-1 ; } public int dfs (TreeNode root,boolean isRight) { if (root==null ){ return 0 ; } int l=dfs(root.left,false ); int r=dfs(root.right,true ); res=Math.max(res,Math.max(l+1 ,r+1 )); if (isRight){ return l+1 ; } return r+1 ; }
Difficulty: 困难
给定一个二叉树,我们在树的节点上安装摄像头。
节点上的每个摄影头都可以监视其父对象、自身及其直接子对象。
计算监控树的所有节点所需的最小摄像头数量。
示例 1:
输入:[0 ,0 ,null,0 ,0 ] 输出:1 解释:如图所示,一台摄像头足以监控所有节点。
示例 2:
输入:[0 ,0 ,null,0 ,null,0 ,null,null,0 ] 输出:2 解释:需要至少两个摄像头来监视树的所有节点。 上图显示了摄像头放置的有效位置之一。
提示:
给定树的节点数的范围是 [1, 1000]。
每个节点的值都是 0。
解法一
树形 DP
func minCameraCover (root *TreeNode) int { var Min = func (a, b int ) int {if a < b {return a}; return b} var INF = 0x3f3f3f3f var dfs func (root *TreeNode) 3 ]int dfs = func (root *TreeNode) 3 ]int { var res [3 ]int if root == nil { return [3 ]int {INF, 0 , 0 } } left := dfs(root.Left) right := dfs(root.Right) res[0 ] = left[2 ] + right[2 ] + 1 res[1 ] = Min(res[0 ], Min(left[0 ]+right[1 ], left[1 ]+right[0 ])) res[2 ] = Min(res[0 ], left[1 ] + right[1 ]) return res } r := dfs(root) return r[1 ] }
树状数组(BIT) 暂时先放在这里,等以后累计多了再单独开辟专题
Difficulty: 困难
给定一个整数数组 nums_,按要求返回一个新数组 _counts_。数组 _counts 有该性质: counts[i] 的值是 nums[i] 右侧小于 nums[i] 的元素的数量。
示例:
输入:nums = [5 ,2 ,6 ,1 ] 输出:[2 ,1 ,1 ,0 ] 解释: 5 的右侧有 2 个更小的元素 (2 和 1 )2 的右侧仅有 1 个更小的元素 (1 )6 的右侧有 1 个更小的元素 (1 )1 的右侧有 0 个更小的元素
提示:
0 <= nums.length <= 10^5
-10^4 <= nums[i] <= 10^4
解法一
这题有 更好的做法 ,直接归并就行了,这里主要是为了学习 BIT
暴力的做法:其实就是桶排序的思想,我们从右向左扫数组,扫描一个就在对应的桶+1,同时计算该位置左边的前缀和,就是右边比当前元素小的值,也就是我们需要的结果,但是问题是这个bit数组是一直在变化的,扫描一个元素就会在 bit 数组对应的位置上+1,每次变化后都需要 O(N) 来重新计算后缀和,这样整体的复杂度就是 O(N^2),数据量 1e5,过不了 OJ
所以我们可以用线段树来维护区间和,但是线段树代码量比较大,常数也比较大,所以这里学一下新科技:**树状数组 **,区间查询,单点修改时间复杂度都是 logN,且代码简单。
同时还有一个问题,这里我们直接按照值来定位是不合适的,数据范围比较大,直接按照元素值来定位会造成很大空间的浪费,并且题目也不允许开这么大的空间,所以还需要离散化,因为我们只关系元素之间的大小关系,所以我们转换成每个元素说对应的 rank 就行了
int [] tree;int n = 0 ;public int lowbit (int i) { return i & -i; } public void update (int i, int delta) { while (i <= n) { tree[i] += delta; i += lowbit(i); } } public int query (int i) { int sum = 0 ; while (i > 0 ) { sum += tree[i]; i -= lowbit(i); } return sum; } public List<Integer> countSmaller (int [] nums) { n = nums.length; tree = new int [n+1 ]; List<Integer> res = new LinkedList <>(); int [] rank = new int [n]; int [][] temp = new int [n][2 ]; for (int i = 0 ; i < n; i++) { temp[i] = new int []{i, nums[i]}; } Arrays.sort(temp, (t1, t2) -> t1[1 ]-t2[1 ]); for (int i = 0 ; i < n; i++) { rank[temp[i][0 ]] = i+1 ; } for (int i = n-1 ; i >= 0 ; i--) { update(rank[i], 1 ); res.add(0 , query(rank[i]-1 )); } return res; }
赞赏
感谢鼓励