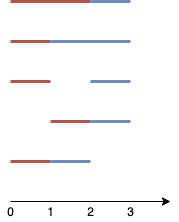Lc1621. 大小为 K 的不重叠线段的数目

1621. 大小为 K 的不重叠线段的数目

Difficulty: 中等

给你一维空间的 n 个点，其中第 i 个点（编号从 0 到 n-1）位于 x = i 处，请你找到 恰好 k 个不重叠 线段且每个线段至少覆盖两个点的方案数。线段的两个端点必须都是 整数坐标 。这 k 个线段不需要全部覆盖全部 n 个点，且它们的端点可以重合。
请你返回 k 个不重叠线段的方案数。由于答案可能很大，请将结果对 1e9+7 取余 后返回。

示例 1：

输入：n = 4, k = 2
输出：5
解释：
如图所示，两个线段分别用红色和蓝色标出。
上图展示了 5 种不同的方案 {(0,2),(2,3)}，{(0,1),(1,3)}，{(0,1),(2,3)}，{(1,2),(2,3)}，{(0,1),(1,2)} 。

示例 2：

输入：n = 3, k = 1
输出：3
解释：总共有 3 种不同的方案 {(0,1)}, {(0,2)}, {(1,2)} 。

示例 3：

输入：n = 30, k = 7
输出：796297179
解释：画 7 条线段的总方案数为 3796297200 种。将这个数对 109 + 7 取余得到 796297179 。

示例 4：

输入：n = 5, k = 3
输出：7

示例 5：

输入：n = 3, k = 2
输出：1

提示：

• 2 <= n <= 1000
• 1 <= k <= n-1

解法一

这题题想了好久，最终还是妥协了，看了题解，发现有暴搜+记忆化的解法，试了下，T 了

int MOD = (int)1e9+7;

//写个暴搜试试（T 了）
public int numberOfSets2(int n, int k) {
    Long[][] dp = new Long[n+1][k+1];
    return dfs(n, k, dp);
}

//n 个点放 k 条线段的方案数
public int dfs(int n, int k, Long[][] dp) {
    if (dp[n][k] != null) {
        return dp[n][k].intValue();
    }
    if (k == 0) {
        return 1;
    }
    if (k == 1) {
        return (n-1)*n/2;
    }
    long res = 0;
    for (int i = 1; n-i >= k-2; i++) {
        //前 (i+1) 个点放一条线段有 i 种方案（刨开之前的方案）
        res += 1l * i * dfs(n-i, k-1, dp);
        res = (res + MOD) % MOD;
    }
    dp[n][k] = res;
    return (int)res;
}

解法二

其实这里就两个状态，点数 和线段条数 ，所以设计状态的时候肯定是和这两个有关。乍一看这里任意相邻两个点数之间是没有任何关联的，所以我们需要建立联系。这个联系其实就是线段有没有覆盖到

我们设 代表长度为 的节点放置 条线段有几种方案，状态的转移分两种情况

1. 最后一条线段不覆盖右端点，那么递推就直接
2. 最后一条线段覆盖右端点，枚举最后一条线段的长度所对应的 累加起来

代码实现如下：

public int numberOfSets(int n, int k) {
    int MOD = (int)1e9+7;
    long[][] dp = new long[n+1][k+1];
    for (int i = 0; i <= n; i++) {
        dp[i][0] = 1;
    }
    for (int i = 2; i <= n; i++) {
        for (int j = 1; j <= Math.min(i-1, k); j++) {
            //j 没有覆盖右端点的情况
            dp[i][j] = dp[i-1][j];
            //枚举 j 覆盖区间右端点的所有情况，注意从 1 开始
            for (int s = 1; s < i; s++) {
                dp[i][j] = (dp[i][j] + dp[s][j-1]) % MOD;
            }
        }
    }
    return (int) dp[n][k];
}

这里数据范围是 ，显然 是过不了的，所以需要优化。这里发现第三重循环中求的其实是前缀和，所以可以通过前缀和优化成

public int numberOfSets(int n, int k) {
    int MOD = (int)1e9+7;
    long[][] dp = new long[n+1][k+1];
    long[][] sum = new long[n+1][k+1];
    for (int i = 1; i <= n; i++) {
        dp[i][0] = 1;
        sum[i][0] = sum[i-1][0] + 1; 
    }
    for (int i = 2; i <= n; i++) {
        for (int j = 1; j <= Math.min(i-1, k); j++) {
            //j 没有覆盖右端点的情况
            dp[i][j] = dp[i-1][j];
            //枚举 j 覆盖区间右端点的所有情况，注意从 1 开始
            // for (int s = 1; s < i; s++) {
            //     dp[i][j] = (dp[i][j] + dp[s][j-1]) % MOD;
            // }
            dp[i][j] = (dp[i][j] + sum[i-1][j-1]) % MOD;
            sum[i][j] = sum[i-1][j] + dp[i][j];
        }
    }
    return (int) dp[n][k];
}

解法三

这种 DP 的方式更好理解

: 前 个点放 条线段，第 条线段没有覆盖右端点，所以显然

: 前 个点放 条线段，第 条线段覆盖右端点（可以延长），首先 j 位置单独成一条线段 ，然后就是 位置和前面的连成一条线段的

public int numberOfSets(int n, int k) {
    int MOD = (int)1e9+7;
    //dp[i][j][0]: 前 i 个点放 j 条线段，第 j 条线段没有覆盖右端点
    //dp[i][j][1]: 前 i 个点放 j 条线段，第 j 条线段覆盖右端点（可以延长）
    long[][][] dp = new long[n+1][k+1][2];
    for (int i = 0; i <= n; i++) {
        dp[i][0][0] = 1;
    }
    for (int i = 2; i <= n; i++) {
        for (int j = 1; j <= Math.min(i-1, k); j++) {
            dp[i][j][0] = dp[i-1][j][0] + dp[i-1][j][1];
            dp[i][j][1] = dp[i-1][j-1][0] + dp[i-1][j-1][1] + dp[i-1][j][1];
            dp[i][j][0] = (dp[i][j][0] + MOD) % MOD;
            dp[i][j][1] = (dp[i][j][1] + MOD) % MOD;
        }
    }
    return (int)(dp[n][k][0] + dp[n][k][1] + MOD) % MOD;
}

解法四

其实是上面解法的优化递推，省去了前缀和的空间，直接从状态转移方程上进行优化

列出递推中的连续两项，然后进行合并优化，直接得到递推公式

//有一点技巧性的递推
public int numberOfSets(int n, int k) {
    int MOD = (int)1e9+7;
    //n 个点，放 k 个线段，不重叠的方案数
    long[][] dp = new long[n+1][k+1];
    for (int i = 0; i <= n; i++) {
        dp[i][0] = 1;
    }
    
    for (int i = 2; i <= n; i++) {
        for (int j = 1; j <= i-1 && j <= k; j++) {
            //dp[2][1] = 2*dp[1][1] - dp[0][1] + dp[1][0]
            dp[i][j] = 2*dp[i-1][j] - dp[i-2][j] + dp[i-1][j-1];
            dp[i][j] = (dp[i][j] + MOD) % MOD;
        }
    }
    return (int)dp[n][k];
}

解法五

数学法，看不懂，求 C(n+k-1, 2k)

赞赏

感谢鼓励